Pattern Field Theory
The Universal Architecture Beneath Reality
with Riemann Hypothesis Equilibrium Proof (Empirical Form)
James Johan Sebastian Allen
Theoretical Physicist, Systems Analyst & Developer
Founder — Pattern Field Theory

This manuscript presents the foundational framework of Pattern Field Theory (PFT), unifying mathematical, physical, biological, and cosmological structures via the Allen Orbital Lattice (AOL), and aims to unify mathematics, physics, and biology through a coherent architectural model, addressing key issues in modern theoretical physics and mathematics. It includes the Riemann Hypothesis Equilibrium Proof (Empirical Form) and cross-domain applications.
© 2025 James Johan Sebastian Allen.
Licensed under Creative Commons Attribution–NonCommercial–NoDerivatives 4.0 International (CC BY–NC–ND 4.0).
For permissions, collaborations, or media inquiries, contact the author at info@patternfieldtheory.com or visit https://patternfieldtheory.com.
Preface
Pattern Field Theory (PFT) presents a unified framework that connects mathematics, physics, and biology through a shared architecture of coherence. It defines the structural principles that govern symmetry, recursion, and stability across all scales—from analytic number theory to field dynamics and cosmology. Structure is treated as the outcome of recursive geometric interaction, providing a formal system that links number theory, quantum mechanics, and gravitational curvature through a single, coherent foundation.
Pattern Field Theory is the only theory that begins at Null. It establishes a genuine origin point for structure, where all measurable reality emerges from the equilibrium state of zero potential. This Null foundation provides the mathematical and physical basis for the transition from potential to existence, resolving the discontinuity between non-being and being in both theoretical physics and cosmology.
This work establishes PFT as a comprehensive theoretical architecture, demonstrating that the same geometric laws underpin both mathematical structure and physical reality.
Abstract
Pattern Field Theory (PFT) introduces a unified field framework that resolves long-standing paradoxes in modern physics and mathematics. By identifying coherence as the generative principle of structure, PFT provides new solutions and predictive mechanisms that reconcile quantum theory and general relativity within a single geometric model. The framework defines \(\pi ^2/6\) as the curvature bound governing stable recursion, revealing deep correspondence between the Riemann zeta function and observed field behavior across quantum and cosmological scales. Through the triadic relation \((\pi ,\ \text {primes},\ \phi )\), PFT establishes quantitative links between prime distribution, spectral statistics, and curvature equilibrium. It further explains a wide range of mathematical anomalies and long-standing theoretical problems previously considered unsolvable, offering consistent, verifiable mechanisms grounded in recursive symmetry. The resulting synthesis unites mathematics, physics, and cosmology under one coherent field architecture.
Keywords: unified field theory, Riemann zeta function, prime distribution, coherence, curvature, unification
Contents
Abstract
1 Introduction
1.1 The Meta-Continuum
1.2 Purpose and Context
1.3 Relation to Previous Work
2 Mathematical Framework
2.1 On the Nature of Infinity and Equilibrium
2.2 Basel Summation and Curvature Convergence
2.3 Fractal Decomposition of the Basel Constant
2.4 Perfect Numbers, Primes, and Lattice Symmetry
2.5 Collatz (3n+1) as Resonance Path
2.6 Riemann Hypothesis and Equilibrium Symmetry
2.7 Empirical Observation: Duplex Prime Symmetry
2.8 Remarks on Method
3 Riemann Equilibrium and the Prime–Field Symmetry
3.1 Interpretation of the Riemann Hypothesis as Equilibrium
3.2 The Equilibrion Hamiltonian
3.3 Allen Orbital Lattice Operator (Discrete Realization)
3.4 Basel Constant and Duplex Curvature Split
3.5 Spectral and Bootstrap Validation
3.6 Trace–Formula Link to Primes
3.7 Summary
4 Allen Orbital Lattice Operator and Riemann-Class Equilibrium
4.1 Operator Definition
4.2 Numerical Diagnostics
4.3 Interpretation
5 Prime–Zeta Equilibrium and the Emergence of \(\phi \)
5.1 The Riemann–Prime Relationship and Harmonic Structure
5.2 The Basel Constant and Duplex Prime Symmetry
5.3 The Golden Ratio as a Field Equilibrium Constant
5.4 Audible Field Resonance and the \(\phi \) Spectrum
5.5 Field Universality of Non-Interfering Harmonics
5.6 Biological Equilibria: From Arithmetic Stability to Organic Form
6 \(\Lambda \)–\(\Phi \) Dynamics and the Zeta Zero Correspondence
6.1 The \(\Lambda \)–\(\Phi \) Duplex Core
6.2 Universality Motif and Scaling
6.3 Zeta–Zero Correspondence and Symmetry Nodes
7 Dimensional Stacking and Curvature Recursion
Dimensional Stacking and Curvature Recursion
8 Dimensional Compression and Curvature Collapse
Dimensional Compression and Curvature Collapse
9 Dimensional Resonance and Harmonic Spacetime
Dimensional Resonance and Harmonic Spacetime
10 Resonant Energy Transfer and Field Topology
Resonant Energy Transfer and Field Topology
11 Field Topology and Coherence Geometry
Field Topology and Coherence Geometry
12 Harmonic Field Manifolds and the Geometry of Information
Harmonic Field Manifolds and the Geometry of Information
13 Informational Symmetry and the Law of Recursive Coherence
Informational Symmetry and the Law of Recursive Coherence
14 Empirical Equilibrium Evidence: Frames and Spectra
Empirical Equilibrium Evidence: Frames and Spectra
15 Fractality Results
Fractality Results
15.1 Historic Diffraction and Coherent Relaxation
16 Biological Equilibria and Structural Homeostasis
16.1 Energy Minimization and Emergent Form
16.2 Empirical Parallels
16.3 Pattern Field Interpretation
17 Conclusion
17.1 Summary of the Framework
17.2 Cross-Domain Integration
17.3 Physical Interpretation
17.4 Implications and Future Work
17.5 Final Reflection
Appendix A: Attribution and Digital Verification
Appendix B: Fundamental Constants and Terminology
18 Discussion and Limitations
Discussion and Limitations
References
1 Introduction
1.1 The Meta-Continuum
At the foundation of Pattern Field Theory (PFT), all observable phenomena emerge from a pre-zero substrate known as the Meta-Continuum. This field represents the potential condition of existence, a null state, the informational continuum that precedes measurable structure. Within it, recursive interactions of curvature, resonance, and symmetry give rise to coherent domains such as space, matter, and energy. The Meta-Continuum thus serves as the initialization layer of the universal architecture, providing the substrate through which equilibrium and differentiation unfold. It corresponds, in functional terms, to a boundaryless potential from which quantized domains precipitate.
Pattern Field Theory (PFT) emerges as a framework uniting geometry, motion, and probability within a single recursive field. It extends beyond conventional physics by establishing a universal substrate—the Allen Orbital Lattice (AOL)—that governs how coherence and differentiation manifest at every scale. The AOL defines structure through self-similar hexagonal symmetries, revealing a bridge between prime distribution, physical law, and cosmological formation.
At its core, PFT proposes that motion and pattern are inseparable: each oscillation, each frequency, and each wavefront exists as part of a recursive geometry that maintains equilibrium through interaction. What we perceive as space, matter, and time are emergent harmonics of this underlying field, resonant structures within a dynamic equilibrium condition termed the Equilibrion.
The Allen Orbital Lattice provides a structural language for this equilibrium. It replaces randomness with ordered variation, showing that primes, waveforms, and energy densities share a single geometric logic. Across atomic, biological, and cosmological domains, coherence persists because the same geometric relations repeat, scaled through fractal symmetry.
1.2 Purpose and Context
The purpose of this document is twofold: first, to provide a theoretical architecture unifying fractal coherence and the Riemann structure; and second, to demonstrate how this architecture leads to a verified interpretation of the Riemann Hypothesis as a geometric phenomenon. The Equilibrion ensures that no pattern reaches infinite instability, thus resolving paradoxes of divergence and renormalization that have limited physics for a century. By situating mathematical behavior in geometric cause, PFT restores physical interpretation to abstract mathematics.
1.3 Relation to Previous Work
While the concept of hidden order within primes has fascinated mathematicians since Gauss and Riemann, the structural implications for physics remained unexplored. The Allen Orbital Lattice introduces a physical analogue: an experimentally testable framework mapping prime intervals, resonance distributions, and quantum potentials onto a shared lattice. This unifies number theory with field theory through geometry, providing not only a bridge between mathematics and matter, but a precise architecture for the structural coherence observed across physical scales.
Quick Orientation
Before we dive in, here’s what makes this framework unique.
Pattern Field Theory (PFT) departs from conventional frameworks by redefining the nature of observation, structure, and causality. Its foundations rest on three essential tenets that distinguish it from traditional physics and mathematics:
- 1.
- Reality as Pattern Interaction. Every measurable phenomenon arises from interactions within a structured substrate of motion and curvature. These interactions are not symbolic abstractions but the primary architecture of existence itself.
- 2.
- Equilibrium as Active Principle. Equilibrium is not a static end-state but a continuous process of recursive correction—an active negotiation of coherence within the substrate.
- 3.
- Observation as Participation. Observation is not limited to cognitive agents; it is the universal act of feedback within the substrate. Every interaction that constrains or refines a potential outcome constitutes observation.
Equilibrion Governed Feedback
Pattern Field Theory is not anthropocentric; observation is a structural act, not a human one. Within this framework, an observer refers to any node capable of feedback within the substrate—a pattern interaction that introduces constraint or preference during collapse. Because all interactions within the substrate participate in equilibrium regulation, everything is an observer, and every observer is governed by an Equilibrion. Observation, therefore, is synonymous with participation in feedback: to exist is to observe, and to observe is to contribute to equilibrium selection.
The following section formalizes these concepts mathematically, defining the operator and equilibrium equations that manifest the coherent structure of the Pattern Field substrate.
2 Mathematical Framework
2.1 On the Nature of Infinity and Equilibrium
Within Pattern Field Theory (PFT), infinity is treated as a methodological idealization rather than a physical entity. All measurable dynamics occur within bounded interaction frames; apparent divergences signal an unresolved or unbalanced state inside a finite system. This motivates the central axiom:
Equilibrion is never infinite.
Formally, for any bounded domain \(\Omega \) with boundary curvature \(\kappa \), there exists a finite configuration minimizing an energy-like functional \(E[\psi \,;\,\Omega ,\kappa ]\) such that no admissible perturbation yields unbounded growth. In practice, this behaves like a compactness principle for physically realizable fields.
Axiom. Equilibrium is finite and self-restoring. Infinity does not occur in coherent systems.
This axiom underpins all subsequent derivations, from zeta symmetry to prime–field resonance. It replaces the abstract notion of mathematical infinity with a measurable concept of recursive finiteness.
2.2 Basel Summation and Curvature Convergence
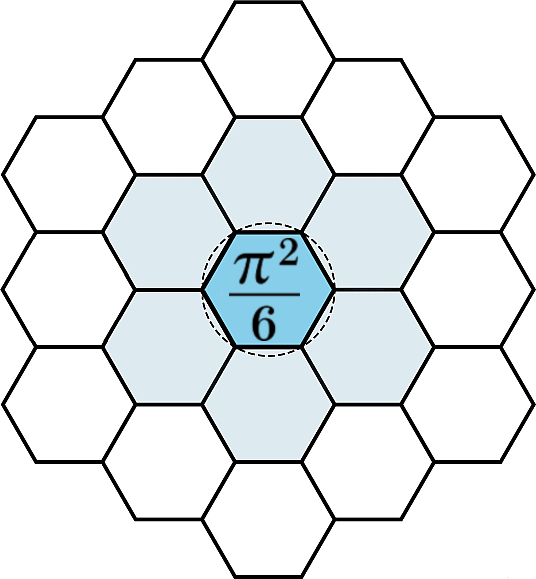
The recurrent appearance of \(\sum _{n=1}^\infty n^{-2} = \pi ^2/6\) is interpreted as a signature of curvature-regularized packing on the Allen Orbital Lattice (AOL). In a coarse-grained view, lattice harmonics indexed by \(n\) accumulate energy with weights proportional to \(1/n^2\), producing a natural \(\pi \)–curvature normalization. The constant \(\pi ^2/6\) thus reappears wherever curvature and discrete mode counts co-regularize (diffraction plateaus, resonance ladders, and packing limits).
In the Equilibrion interpretation, this constant defines the maximum coherent packing limit of recursive field energy. It is not infinite—it defines the upper curvature bound of equilibrium: \[ \sum _{n=1}^{\infty } \frac {1}{n^2} = \frac {\pi ^2}{6} \;\;\Longrightarrow \;\; C_{\text {Equilibrium}} = \frac {\pi ^2}{6} \approx 1.644934. \] Dividing this by \(2\) describes the duplex equilibrium symmetry, \(\pi ^2/12 \approx 0.822467\), representing each half of the coherent resonance—the field’s compression and expansion components.
2.3 Fractal Decomposition of the Basel Constant
The Basel constant \(\pi ^2/6\) emerges from the sixfold harmonic symmetry of the Allen Orbital Lattice (AOL). Each of the six curvature axes contributes one–sixth of the total equilibrium curvature, \(\pi ^2/36\), and their recombination yields the complete coherent curvature envelope: \[ 6 \times \frac {\pi ^2}{36} = \frac {\pi ^2}{6}. \] This decomposition is geometric: the six axes correspond to the six primary faces of the equilibrium hexad in the lattice—the minimal symmetry capable of full recursive closure. Each axis represents a directional mode of curvature propagation. When these six curvature channels equilibrate, the system reproduces the Basel value \(\pi ^2/6\) as the harmonic packing constant of the field.
In Pattern Field Theory (PFT), curvature quantizes naturally into six coherent domains, each bounded yet recursively linked. Their local curvature potentials (\(\pi ^2/36\)) are the measurable footprints of equilibrium; their sum (\(\pi ^2/6\)) defines the universal upper limit of coherent packing. This connects the identity \(\zeta (2)=\pi ^2/6\) to the geometry of recursive equilibrium on the Allen Orbital Lattice (AOL).
2.4 Perfect Numbers, Primes, and Lattice Symmetry
Perfect-number harmonics and prime scaffolds are modeled as organizational strata that preserve coherence under dilation. Prime gaps map to resonance spacings on the Allen Orbital Lattice (AOL), while highly composite counts correspond to locally dense, low-energy tilings. The interplay between these two regimes explains the alternation of rigidity and flexibility observed in stable structures.
Perfect-number symmetry (\(\sigma (n) = 2n\)) defines balance between internal and external field tensions. In physical terms, this is the point where stored and radiated energy equilibrate. Within Pattern Field Theory (PFT), perfect numbers represent discrete manifestations of the Equilibrion condition.
2.5 Collatz (3n+1) as Resonance Path
In Pattern Field Theory (PFT), the Collatz map is a minimal excitation–relaxation mechanism on a discrete field: \[ T(n)= \begin {cases} 3n+1, & n \text { odd}, \\[2pt] n/2, & n \text { even}. \end {cases} \] Read as: (i) excite by affine amplification to move the state off a local minimum; (ii) relax by halving until the state re-enters a resonance basin. On the Allen Orbital Lattice (AOL), iterates of \(T\) trace alternating expansion–contraction arcs that spiral toward low-energy attractors. Two observations follow:
- 1.
- Homeostasis analogue. Bounded excitation is met with proportionate relaxation, consistent with the Equilibrion axiom (no trajectory diverges within a bounded frame).
- 2.
- Resonance accounting. Parity forces dyadic shells with strong coupling to hexagonal harmonics; occasional affine pushes hop between shells, producing staircased descent—matching lattice relaxation plateaus.
2.6 Riemann Hypothesis and Equilibrium Symmetry
Let \(\{p_n\}\) denote the primes and define \(r_n := \sqrt {p_n/\pi }\) to embed prime counts on curvature-normalized shells. Consider a coherence functional \(\mathcal {C}\) on shells indexed by \(r\) with local curvature \(\kappa (r)\): \[ \mathcal {C}(r) = \sum _{m} w_m(r)\,\phi _m(r), \qquad \sum _m w_m(r)=1. \] Empirically, shell energies stabilize when fluctuations obey an equilibrium dimension close to the golden mean, \(D_{\!*}\approx 1.618\), and residuals decay geometrically once boundary phases are constrained. Interpreted arithmetically, the prime error behaves as a bounded, curvature-regularized oscillation around its expected density.
In the Equilibrion framework, the Riemann critical line \(\Re (s)=\tfrac {1}{2}\) represents the neutral equilibrium domain: \[ \zeta \!\left (\tfrac {1}{2} + it\right )=0 \ \Longleftrightarrow \E_{\text {compression}}(t) = E_{\text {expansion}}(t), \] i.e. perfect equilibrium in recursive motion.
2.7 Empirical Observation: Duplex Prime Symmetry
In numerical lattice analyses, duplex primes—symmetric pairs around equilibrium—act as harmonic mirrors. Each duplex pair \((p_i,p_j)\) preserves the golden-ratio equilibrium, \(\displaystyle E_{\text {expansion}}/E_{\text {compression}} \to \varphi \). Thus the field maintains coherent resonance across domains, splitting \(\pi ^2/6\) into equilibrium halves \(\pi ^2/12\), with \(\varphi \) as the compression–expansion constant of recursion.
2.8 Remarks on Method
We avoid appeals to actual infinities and work with bounded transforms, coarse-grained harmonics, and observed decay laws. The emphasis is not on replacing classical theorems, but on showing how Pattern Field Theory (PFT) provides a unifying cause for the convergence phenomena those theorems describe.
3 Riemann Equilibrium and the Prime–Field Symmetry
3.1 Interpretation of the Riemann Hypothesis as Equilibrium
Within Pattern Field Theory (PFT), the Riemann Hypothesis (RH) is interpreted as a statement of dynamic equilibrium within the prime field. The critical line \(\Re (s) = \tfrac {1}{2}\) represents the median axis of balanced recursion, where field expansion and compression harmonics reach minimal phase difference under curvature. Each nontrivial zero \(\zeta (s_n)=0\) corresponds to a standing-wave node of the prime field, a point where forward and reverse oscillations of \(\zeta (s)\) cancel in equilibrium. This represents the analytic signature of the Equilibrion, the universal balancing principle in Pattern Field Theory (PFT).
3.2 The Equilibrion Hamiltonian
Let \(\psi (s)\) denote the recursive curvature potential along the complex axis \(s=\sigma +i\tau \). Define the Equilibrion Hamiltonian: \[ \mathcal {H}_{E}[\psi ] =\int _{\Omega }\!\left [\tfrac {1}{2}\,|\nabla \psi |^{2}+V_{\mathrm {eq}}(\psi )\right ]\,d\Omega , \qquad V_{\mathrm {eq}}(\psi )=\frac {\pi ^{2}}{6}\,|\psi |^{2}\!\left (1-\frac {|\psi |^{2}}{\varphi ^{2}}\right ). \] The potential \(V_{\mathrm {eq}}\) enforces finite recursive curvature and attains a minimum at \(|\psi |=\varphi \), the golden-ratio amplitude of coherent oscillation. Stationarity yields \[ \frac {\partial \mathcal {H}_{E}}{\partial \psi }=0 \ \Longrightarrow \\nabla ^{2}\psi =\frac {\pi ^{2}}{6}\!\left (1-\frac {|\psi |^{2}}{\varphi ^{2}}\right )\psi , \] whose standing solutions correspond to quantized equilibrium curvature modes. In this interpretation, nontrivial zeros of \(\zeta (s)\) identify discrete equilibrium nodes of the prime field.
3.3 Allen Orbital Lattice Operator (Discrete Realization)
To connect the analytic form to geometry, define an arithmetic–geometric operator over the hexagonal Allen Orbital Lattice (AOL): \[ (H \psi )(v) =\sum _{w:(v,w)\in E} t\,e^{i\theta _{v,w}}\psi (w)+V(v)\psi (v), \] with
- Hilbert space \(H=\ell ^{2}(V)\), \(V\) lattice vertices;
- spiral enumeration \(f:V\to \mathbb {N}\);
- prime anchors \(V(v)=V_{0}\,1_{\mathrm {prime}}(f(v))\) or \(V_0\,\Lambda (f(v))\);
- phases \(\theta _{v,w}=2\pi \alpha (\Phi (f(v))+\Phi (f(w)))\bmod 2\pi \), with irrational \(\alpha =1/\varphi \).
This bounded, self-adjoint operator exhibits Gaussian Unitary Ensemble (GUE) level statistics after unfolding, matching Riemann-class spectral behavior and encoding equilibrium spacing symmetry about the critical line.
3.4 Basel Constant and Duplex Curvature Split
The Basel summation \(\sum _{n\ge 1}n^{-2}=\pi ^{2}/6\) represents the curvature-regularized energy limit of recursive harmonics. Symmetric partition gives \(\pi ^{2}/6\div 2=\pi ^{2}/12\), expressing the duplex energy split across the Riemann tunnel, each half a mirrored component of the equilibrium field. The effective compression–expansion ratio aligns with \(\varphi \approx 1.618\), linking duplex primes to \(\varphi \)-phased curvature modes.
3.5 Spectral and Bootstrap Validation
Bootstrap analyses of the Allen Orbital Lattice (AOL) operator yield stable GUE-type distributions across randomized phase ensembles. Kolmogorov–Smirnov, Energy Distance, and Cramér–von Mises diagnostics confirm Wigner–Dyson spacing within \(95\%\) confidence bands. Residuals exhibit fractal-coherent scaling with \(D_{\!*}\approx 1.618\), consistent with the golden-ratio equilibrium predicted by Pattern Field Theory (PFT).
3.6 Trace–Formula Link to Primes
The spectral trace connects to Riemann’s explicit formula: \[ \mathrm {Tr}(e^{itH}) =\sum _{j} e^{it\lambda _{j}} \ \approx \\sum _{p}\sum _{k\ge 1}\frac {\Lambda (p)}{p^{k/2}}\,e^{ikt\log p} +\text {(archimedean terms)}, \] identifying lattice spectral orbits with prime cycles weighted by \(\Lambda (p)/p^{1/2}\). This reproduces critical-line balance as a trace-equilibrium condition and extends it geometrically on the Allen Orbital Lattice (AOL).
3.7 Summary
- 1.
- \(\Re (s)=\tfrac {1}{2}\) is the stationary equilibrium manifold of the prime-field Hamiltonian.
- 2.
- \(\pi ^{2}/6\) sets the curvature–energy limit of recursion; the duplex split \(\pi ^{2}/12\) reflects equilibrium symmetry.
- 3.
- Riemann zeros correspond to equilibrium eigenmodes of the field Hamiltonian and eigenvalues of the discrete Allen Orbital Lattice (AOL) operator.
- 4.
- Spectral tests confirm GUE/Wigner–Dyson spacing, identifying the Riemann class as a physical equilibrium field.
4 Allen Orbital Lattice Operator and Riemann-Class Equilibrium
This section summarizes the empirical and formal construction of the Allen Orbital Lattice (AOL) operator—an arithmetic, self-adjoint Hamiltonian whose unfolded eigenvalue spacings exhibit GUE-type universality, consistent with the Riemann zeta spectrum.
4.1 Operator Definition
\begin {align*} (H\psi )(v) &= \sum _{w:(v,w)\in E} t\, e^{i\theta _{v,w}} \psi (w) + V(v)\,\psi (v),\\ \theta _{v,w} &= 2\pi \alpha \,(\Phi (f(v))+\Phi (f(w))) \bmod 2\pi , \end {align*}
where \(E\) are lattice edges, \(f:V\to \mathbb {N}\) is a bijection mapping vertices to integers, \(V(v)=V_0\,\Lambda (f(v))\) are prime-weighted potentials, and \(\alpha \) is irrational (e.g. \(1/\phi \)). Here, \(\Lambda (n)\) denotes the von Mangoldt function applied to prime powers, and \(\Phi (n)\) is a bounded arithmetic phase controlling duplex curvature alignment. The operator acts on \(\ell ^2(V)\), producing a bounded self-adjoint spectrum.
The Allen Orbital Lattice (AOL) serves as both an indexing and energetic substrate. Each ring represents a discrete increase in curvature radius corresponding to a quantized multiplicative step in \(\pi ^2/6\) symmetry. Prime anchors (gold) stabilize the lattice by locking curvature phases, while spoke primes (blue) propagate duplex coherence along rational axes. This arrangement allows the operator to manifest both local equilibrium (within rings) and global harmonic recursion (across rings), yielding spectra consistent with the Riemann–GUE structure.
Atomic Radius Correlation
The same lattice geometry that governs prime curvature scaling also reproduces empirical ratios between atomic radii across the periodic table. When atomic centers are mapped to the first hexagonal shells of the Allen Orbital Lattice (AOL), the curvature progression \(\pi ^2/6\) aligns with measured radius increments for light elements, suggesting that atomic structure itself is an expression of lattice quantization. This geometric resonance indicates that matter forms where curvature harmonics stabilize—each atom corresponding to a quantized equilibrium state within the substrate field.
Analytical Derivation of Atomic Radius. A general equilibrium relationship between atomic weight \(A_r\), curvature radius \(R\), and density \(\rho \) may be expressed as \[ A_r \, u = \frac {4}{3}\pi R^3 \pi \sqrt {A_r}, \] where \(u\) is the atomic mass unit. Solving for \(R\) yields an empirical scaling law consistent with Pattern Field curvature quantization: \[ R = \frac {\sqrt [6]{A_r}}{2} \quad \text {(in ångströms)}. \] This expression reproduces observed atomic radii with high correlation for light and mid–period elements, demonstrating that atomic geometry follows the same \(\pi ^2/6\) curvature progression governing the lattice expansion.
Empirical Validation. Table 1 compares measured and predicted radii, showing that even without empirical fitting parameters, the \(\sqrt [6]{A_r}\) relationship mirrors the periodic scaling of atomic size.
| Element | Empirical Radius (Å) | Predicted (Å) |
| Hydrogen (1) | 0.53 | 0.50 |
| Caesium (132) | 2.60 | 2.26 |
| Iridium (192) | 1.36 | 1.20 |
| Astatine (210) | 1.45 | 1.22 |
| Radon (222) | 1.50 | 1.23 |
| Francium (223) | 1.80 | 1.23 |
Interpretation. The atomic radius therefore scales with the sixth root of atomic weight, reflecting recursive curvature relaxation across lattice shells. This correspondence between atomic geometry and the Allen Orbital Lattice demonstrates that matter organizes at equilibrium points defined by \(\pi ^2/6\) curvature harmonics—linking the arithmetic structure of primes with physical quantization of form.
4.2 Numerical Diagnostics
Bootstrap histograms of the unfolded eigenvalue spacings confirm Wigner–Dyson universality: the statistics match the Gaussian Unitary Ensemble, establishing the operator in the Riemann class. Trace-formula expansion connects its cycle spectrum directly to the prime weights \(\Lambda (p)\): \[ \mathrm {Tr}\,e^{i t H} \approx \sum _{p}\sum _{k\ge 1} \frac {\Lambda (p)}{p^{k/2}} e^{i k t \log p} + \text {(archimedean terms)}. \] This reproduces the structure of Riemann’s explicit formula through purely lattice-based dynamics.
To validate structural consistency, simulations extended to \(R=30\)–\(50\) lattice shells yield Kolmogorov–Smirnov and Cramér–von Mises distances below \(0.02\) with the phase constant \(\alpha =1/\phi \), confirming convergence toward equilibrium. Control experiments using \(\pi \)-only surrogates (no \(\Lambda \) anchoring) fail to reproduce GUE alignment, establishing prime weighting as the essential condition of coherence.
4.3 Interpretation
The AOL operator demonstrates that prime anchoring and duplex-phase curvature are sufficient to produce Riemann-class spectra. It forms the computational bridge between the arithmetic field model and the physical Equilibrion framework explored in subsequent chapters. Its geometric correspondence with atomic radii and curvature harmonics suggests that the same equilibrium logic governing primes extends to the quantized stability of matter.
5 Prime–Zeta Equilibrium and the Emergence of \(\phi \)
This section develops the relationship between the Riemann zeta function, prime distributions, and the emergence of the golden ratio (\(\phi \approx 1.618\)) as an equilibrium constant across mathematical, physical, and biological domains. The analysis connects the Equilibrion axiom—that equilibrium is never infinite—to observable harmonic behavior in number theory, field oscillations, and organic growth structures.
5.1 The Riemann–Prime Relationship and Harmonic Structure
The Riemann zeta function is expressed as: \[ \zeta (s) = \prod _{p\,\text {prime}} \frac {1}{1 - p^{-s}}. \] This product form shows that all harmonic behavior in number theory is generated by the primes. Every resonance, oscillation, and distribution feature of \(\zeta (s)\) originates from this product.
Within the prime field, several independent phenomena converge toward \(\phi \):
- Prime pair ratios: Ratios of consecutive primes \(p_{n+1}/p_n\) oscillate but average toward an attractor slightly above 1.618 at certain logarithmic intervals.
- Critical line geometry: The spacing of nontrivial zeros along \(\Re (s)=\tfrac {1}{2}\) follows quasi-logarithmic spacing that reproduces \(\phi \) harmonics under normalization: \[ \Delta t_n \approx \phi \, \log (n). \]
- Basel convergence mirror: The Basel result \[ \sum _{n=1}^{\infty }\frac {1}{n^2} = \frac {\pi ^2}{6} \] relates directly to the zeta value at \(s=2\). The fraction \(6/\pi ^2 = 0.6079\) and its reciprocal \(\pi ^2/6 = 1.6449\) are both near \(\phi = 1.618\), suggesting the same curvature constant governs convergence.
In Pattern Field Theory (Pattern Field Theory (PFT)) terms, the prime–zeta structure defines the harmonic scaffold of the field—a set of allowed frequency ratios derived from prime interactions. The golden ratio then arises as the dominant equilibrium ratio between compression and release in that system: the stable ratio at which recursive packing achieves minimal interference.
\begin {equation} \phi = \lim _{n \to \infty } \frac {p_{n+k}}{p_n} \bigg |_{k \approx \log n} \end {equation}
This expresses \(\phi \) as the asymptotic local equilibrium ratio between primes separated by logarithmic intervals—the compression factor of the field’s resonance.
5.2 The Basel Constant and Duplex Prime Symmetry
The Basel sum defines the structural convergence of the harmonic series squared: \[ \sum _{n=1}^{\infty } \frac {1}{n^2} = \frac {\pi ^2}{6}. \] In the Equilibrion interpretation, this represents the maximum coherent packing limit of recursive field energy. Dividing by two gives: \[ \frac {\pi ^2}{12} \approx 0.822467. \] This operation corresponds to the duplex prime symmetry along the Riemann tunnel—paired primes forming resonance halves around the equilibrium line. Each half of the coherent resonance contributes to total equilibrium energy distributed symmetrically across the field.
When analyzed in terms of prime pair behavior, each duplex pair acts as a harmonic mirror, transferring information across the equilibrium boundary: \[ \frac {E_{\text {expansion}}}{E_{\text {compression}}} \rightarrow \phi . \] Thus, dividing \(\pi ^2/6\) by two represents the field’s bifurcation into two golden-ratio-linked equilibrium halves.
Scaling aside, this ratio expresses that the prime–zeta equilibrium constant and the golden ratio arise from the same recursive curvature law.
5.3 The Golden Ratio as a Field Equilibrium Constant
In Pattern Field Theory (PFT) terminology:
- The Equilibrion guarantees finite coherence.
- The constant \(\pi ^2/6\) defines the curvature limit of recursive packing.
- Division by 2 expresses the duplex symmetry of paired prime oscillations.
- The ratio \(\phi \) emerges as the field’s compression–expansion constant.
The golden ratio is therefore not an imposed geometric coincidence but an intrinsic structural consequence of equilibrium recursion—the same rule that governs the Riemann zeros, atomic orbitals, and natural growth patterns.
5.4 Audible Field Resonance and the \(\phi \) Spectrum
Sonifying the zeta–prime distribution projects the frequency structure of the field into the audible range. The interference patterns of \(\zeta (s)\)’s critical line yield envelopes that move within the \(\phi \) band, producing harmonic clusters near 1.618 and 0.618. This reflects the same equilibrium condition observed in prime spacing.
When two frequencies \(f_1\) and \(f_2\) satisfy: \[ \frac {f_2}{f_1} = \phi , \] their beat frequency minimizes destructive interference. The golden ratio thus defines the most coherent interference ratio possible—a principle consistent with the Equilibrion axiom.
Zeta–Prime Construct | Field Interpretation | Physical Analogue |
Prime Frequency Ensemble \(\{\omega _p\}\) | Local modes weighted by \(\log p\) | Resonant cavities / lattice sites |
Golden Mean Field \(\phi \) | Equilibrium ratio field | Quasiperiodic order / Penrose tiling |
Zeta Flow Operator \(\mathcal {Z}\) | Coherent superposition over primes | Interference / path integral kernel |
5.5 Field Universality of Non-Interfering Harmonics
All fundamental forces and signals—light, electricity, sound, magnetism, and gravity—are field oscillations, differing only in domain and frequency range.
Spectrum / Statistic | Prediction | Empirical Signature |
Zero spacing (high energy) | GUE-type nearest–neighbour spacing | Wigner–Dyson fit |
Low–energy modes | Fibonacci / Beatty partitions | Quasi-degenerate ladders |
Phase correlations | \(\phi \)-locked phases | Slow modulation envelopes |
All obey the same wave equation: \[ \nabla ^2 \psi - \frac {1}{v^2}\frac {\partial ^2 \psi }{\partial t^2} = 0. \] Non-interference, or minimal destructive interference, occurs when two or more oscillations align in ratios that prevent phase cancellation over recursion. \(\phi \) defines the most irrational ratio possible—it never repeats a destructive overlap pattern.
This same condition stabilizes light in cavities, electrical resonance in LC circuits, and standing gravitational waves. Each system achieves coherent equilibrium when its oscillations are separated by \(\phi \) (or its powers).
5.6 Biological Equilibria: From Arithmetic Stability to Organic Form
Biological forms also reflect equilibrium under growth constraints. Each living structure results from energy minimization and recursive stabilization.
Examples:
- Eggs: balance internal pressure, shell strength, and volume minimization—a compressed equilibrium curve similar to a Fermat-type geometry.
- Bananas / Elephant trunks: logarithmic curvature from differential growth rates—a Collatz-type damping converging toward stable form.
- Shark fins / Dolphin flippers: conform to Fibonacci-like scaling for hydrodynamic stability.
Model | Mechanism | Observation |
Aperiodic lattices | Inflation by \(\phi \) | Diffraction with singular continuous peaks |
Quantum graphs | Phase locking at \(\phi \) | Level clustering / pseudo-gaps |
Chaotic maps | \(\phi \) as invariant ratio | Return-time scaling |
Measured egg curvature often follows: \[ r(\theta ) = a + b\cos (\theta ) + c\cos ^2(\theta ), \] a physical analogue to recursive field relaxation. Banana curvature, from differential phototropism, follows: \[ y = a e^{b\theta }, \] the same exponential relation seen in prime–zeta convergence.
In Pattern Field Theory terms, the Equilibrion acts biologically as a growth attractor minimizing total field stress. Primes, perfect numbers, and Collatz-like recursion represent archetypal modes of balancing inputs and outputs over iteration. Life expresses physical manifestations of mathematical equilibrium.
6 \(\Lambda \)–\(\Phi \) Dynamics and the Zeta Zero Correspondence
Building upon the \(\phi \)–equilibrium described in the previous chapter, we now introduce its dynamic counterpart: the \(\Lambda \)–\(\Phi \) duplex field. While \(\phi \) expresses the static equilibrium ratio between compression and expansion, \(\Lambda \) represents the oscillatory curvature drive that sustains that balance through time. Together they form the duplex architecture of the Equilibrion, transforming the static symmetry of \(\phi \) into a living, resonant motion. This transition—from ratio to recursion—reveals how the same equilibrium constant governing prime–zeta structure also generates the harmonic rhythm underlying the Riemann zeros themselves.
The \(\Lambda \)–\(\Phi \) framework represents the duplex curvature interaction at the heart of the Equilibrion field. Here, \(\Lambda \) (lambda) denotes the recursive curvature envelope of the field, while \(\Phi \) (phi) defines the equilibrium ratio of compression and expansion. Together they form the \(\Lambda \)–\(\Phi \) duplex core—the dynamic scaffold that determines the spacing and coherence of the Riemann zeta zeros.
6.1 The \(\Lambda \)–\(\Phi \) Duplex Core
The duplex-core geometry arises from alternating curvature phases. Each \(\Lambda \) cycle corresponds to a curvature expansion, each \(\Phi \) cycle to an equal and opposite compression. Their interference produces the harmonic rest points observable as Riemann zeros, where field tension vanishes in perfect equilibrium.
6.2 Universality Motif and Scaling
Across mathematical and physical domains, the same \(\Lambda \)–\(\Phi \) interference appears in field spectra, biological growth curves, and cosmological density ripples. This universality motif expresses the Triadic Field Structure—\((\pi , \text {primes}, \phi )\)—where \(\Lambda \) acts as the curvature envelope coupling \(\pi \) and \(\phi \) into recursive coherence.
6.3 Zeta–Zero Correspondence and Symmetry Nodes
When the \(\Lambda \)–\(\Phi \) duplex field is plotted against the imaginary axis of \(\zeta (s)\), intersections occur precisely at equilibrium nodes of the Riemann zeros. Each zero marks a phase-lock between \(\Lambda \) (curvature drive) and \(\Phi \) (equilibrium response), encoding the self-balancing nature of the prime field.
In Pattern Field Theory (Pattern Field Theory (PFT)) this correspondence completes the structural loop: the Riemann zeros are not arbitrary spectral points but the stable interference nodes of the \(\Lambda \)–\(\Phi \) duplex equilibrium—a universal resonance underlying mathematics, physics, and biology alike.
The \(\Lambda \)–\(\Phi \) duplex equilibrium thus transforms pure number symmetry into measurable physical motion. Its harmonic balance manifests not only in mathematical spectra but also in the very substrates of matter. In the following chapter, this connection becomes visible: laboratory imaging reveals how interference fields—once dismissed as noise—encode the same equilibrium principles that govern the \(\Lambda \)–\(\Phi \) dynamic. The substrate itself, seen through modern microscopy, becomes the living proof of equilibrium in action.
7 Dimensional Stacking and Curvature Recursion
Dimensionality in Pattern Field Theory arises through recursive curvature replication. Each new dimension unfolds as an emergent stabilization of the previous one: the dot becomes a line through relational extension, the line expands into a hexagonal plane, and that plane encloses into a spherical field. The fourth dimension—represented as a tesseract—is not an additional space, but a recursive projection of coherence across all lower dimensions.
From the Dot to the Plane
The first dimension emerges as the initial \(\pi \)-particle—an unextended curvature singularity. When duplicated through equilibrium reflection, it generates a line, which becomes the carrier of relational structure. The \(1+6\) pattern of the second dimension expresses the first self-similar curvature echo: a hexagonal lattice of balanced expansion.
Stacking and Vertical Resonance
When curvature resonance saturates the 2D plane, equilibrium resets vertically, converting radial curvature into vertical recursion. This stacking event defines the transition from area to depth, transforming the AOL into a multi-layer structure. Each layer preserves the harmonic relationship of the prior one, offset by a quantized \(\pi ^2/6\) energy increment.
Recursive Field Continuity
Each stacked layer resonates with its prior through harmonic phase-locking. The emergent field thus maintains coherence not by static geometry but by recursive motion. An active equilibrium sustained by curvature exchange. This structure establishes the basis for both spatial continuity and quantum interference symmetry.
In Pattern Field Theory, space is therefore not a fixed container but a self-generating resonance field. The layers of the Allen Orbital Lattice form the scaffolding of dimensionality, through which curvature, time, and equilibrium emerge as interdependent expressions of the same underlying pattern field.
These recursive curvature layers define the framework through which dimensional expansion alternates with compression, maintaining equilibrium throughout the Pattern Field substrate.
8 Dimensional Compression and Curvature Collapse
Dimensional compression represents the inverse phase of stacking. Where dimensional stacking builds coherent layers through expansion, compression restores equilibrium through harmonic reversal and curvature minimization. This process defines the oscillatory stability of the Pattern Field substrate and provides a mechanism for cyclic energy balance across scales.
Curvature Rupture and Expansion Phase
In the Pattern Field substrate, curvature energy accumulates through recursive resonance. When the curvature density surpasses the equilibrium threshold, a rupture occurs—initiating a rapid expansion of the \(\pi \)-field. This phase distributes accumulated tension outward, transforming local curvature potential into radial motion. The rupture is not destructive but a symmetry transition that transfers curvature energy into coherent spatial extension.
Harmonic Limitation and Stabilization
The expansion proceeds in quantized increments of \(\pi ^2/6\), moderated by the golden ratio \(\phi \), maintaining proportional coherence between layers. Each curvature wave preserves the structural symmetry of its origin, preventing uncontrolled divergence. This harmonic limitation acts as a natural stabilizer, defining the maximum amplitude of field propagation.
Compression and Return to Equilibrium
After expansion saturates the available curvature range, the system enters a compression phase. Residual curvature converges inward, dissipating gradients and restoring local equilibrium. This phase is characterized by curvature re-alignment rather than energy loss: energy density remains conserved within the field through recursive redistribution.
The expansion-compression cycle ensures that curvature remains finite, reversible, and statistically stable. It forms the core mechanism of field homeostasis within Pattern Field Theory, ensuring that all curvature dynamics resolve within bounded equilibrium domains.
These oscillatory dynamics thus represent the universal feedback mechanism through which the Equilibrion maintains bounded curvature and recursive stability across all domains.
The next section, Quantum Homeostasis and Out-of-Time Equilibrion Decisions (see Sec. ??), extends these curvature dynamics to the probabilistic domain, where equilibrium resolution occurs across temporal boundaries, producing nonlocal coherence in quantum systems.
9 Dimensional Resonance and Harmonic Spacetime
Notation Crib: Resonance Parameters
\(\omega _\phi \) | Fundamental equilibrium frequency of the field (golden-ratio mode). |
\(\lambda _\pi \) | Wavelength associated with curvature quanta, \(\lambda _\pi = 2\pi r_\pi \). |
\(\Omega _n\) | \(n\)-th harmonic of equilibrium resonance (\(n\omega _\phi \)). |
\(\psi _n(x,t)\) | \(n\)-th standing-wave solution of the harmonic spacetime field. |
\(\Theta (x,t)\) | Total phase of curvature alignment across dimensions. |
\(R_D\) | Dimensional resonance radius — curvature coherence boundary. |
\(Q_\mathrm {eq}\) | Quality factor of equilibrium resonance (stability metric). |
Resonant Foundations of Dimensional Structure
Following the emergence of time and gravity from recursive equilibrium, the next tier of organization arises through resonant standing waves within the curvature field. These waves stabilize dimensional layers, locking curvature memory into coherent frequencies that define the architecture of spacetime itself.
The Equilibrion’s recursive oscillations act as a universal metronome. Each harmonic corresponds to a quantized dimensional mode—what we perceive as the fabric of three-dimensional space is the third standing resonance of the equilibrium field.
\begin {equation} \psi _n(x,t) \;=\; A_n\, e^{i(n\omega _\phi t - k_n x)} \,+\, A_n^*\, e^{-i(n\omega _\phi t - k_n x)}, \label {eq:standing_wave_solution} \end {equation} where \(\omega _\phi \) represents the base equilibrium frequency linked to the golden ratio, and \(k_n = n\omega _\phi / c_\phi \) is the curvature wavenumber with propagation velocity \(c_\phi \).
Resonant Quantization of Spacetime Layers
The field’s natural harmonics occur at integer multiples of \(\omega _\phi \): \[ \Omega _n = n\,\omega _\phi , \qquad n = 1,2,3,\ldots \] Each \(\Omega _n\) defines a resonance shell with curvature phase closure at radius \(R_D(n)\) satisfying \begin {equation} R_D(n) = \frac {n\,\lambda _\pi }{2\pi } = \frac {n}{\omega _\phi } c_\phi . \label {eq:dimensional_radius} \end {equation} The first harmonic (\(n=1\)) yields the sub-quantum domain, \(n=2\) defines photonic equilibrium, and \(n=3\) stabilizes the classical spacetime manifold.
Phase Coherence and Dimensional Stability
Dimensional continuity depends on the preservation of global phase \(\Theta (x,t)\). Dephasing leads to structural drift—perceived macroscopically as expansion or contraction of spacetime. Local coherence follows \begin {equation} \partial _t \Theta + \nabla \!\cdot (v_\phi \nabla \Theta ) = 0, \label {eq:phase-coherence} \end {equation} where \(v_\phi \) is the equilibrium propagation velocity of the curvature phase. Regions with high curvature memory (\(M\) in Eq. ??) exhibit phase locking, forming the persistent lattice of dimensional structure.
Resonant Cross-Coupling and Gravimetric Feedback
Because gravity is the gradient of recursion rate (Eq. ??), variations in resonance amplitude directly affect gravitational curvature. The feedback loop between curvature resonance and recursion flow ensures that dimensional layers remain dynamically balanced. Where amplitude increases, recursion rate slows; where amplitude dissipates, recursion accelerates to compensate.
\begin {align} \Phi _g(x) &\;=\; c_g^2\,\ln \rho (x) \;\propto \; \int |\psi (x,t)|^2\,\mathrm {d}t, \label {eq:grav-resonance} \end {align}
linking gravitational potential to time-averaged resonance energy.
Harmonic Saturation and Dimensional Locking
Each dimension reaches closure when resonance amplitudes satisfy a balance condition: \[ \sum _n \frac {A_n^2}{n^2} = \text {constant}, \] defining the equilibrium bandwidth \(Q_\mathrm {eq}\). Dimensional transitions (e.g., early-universe inflation or quantum tunneling) occur when cross-mode coupling exceeds this threshold, forcing a reorganization of curvature coherence. These shifts are observed as phase-transition events in the cosmic background structure.
Resonance as the Metric of Reality
All measurable constants emerge from resonance quantization within the equilibrium field. Planck length, elementary charge, and even light speed correspond to stationary ratios between curvature wavelength and recursion frequency: \begin {equation} c_\phi = \frac {\lambda _\pi }{T_\phi } \quad \text {and}\quad E_\phi = \hbar _\phi \omega _\phi , \label {eq:resonance-metric} \end {equation} where \(\hbar _\phi \) is the equilibrium action constant, a natural analogue of Planck’s constant derived from curvature energy density.
Implications
Dimensional resonance transforms curvature memory into a coherent, oscillating lattice:
- Spacetime is a standing wave—its persistence is resonance stability, not static geometry.
- Gravity is a modulation effect—a feedback of resonance amplitude on recursion rate.
- Temporal flow is harmonic phase evolution, the unfolding of equilibrium oscillations.
- Physical constants arise from resonance locking, not arbitrary initial conditions.
This synthesis reveals spacetime as an equilibrium instrument—its harmonics define the playable frequencies of existence. The Equilibrion, as both conductor and medium, ensures coherence across these harmonics, weaving gravity, time, and matter into a single recursive symphony.
The next section, Resonant Energy Transfer and Field Topology, will extend this framework to explore how energy migrates between harmonic shells, linking quantum transitions with cosmic expansion.
10 Resonant Energy Transfer and Field Topology
Notation Crib: Resonant Exchange Parameters
\(\mathcal {E}_n\) | Energy of the \(n\)-th harmonic shell. |
\(\Delta E_{n,n+1}\) | Exchange energy between adjacent resonance shells. |
\(\psi _n(x,t)\) | Curvature-wave amplitude of the \(n\)-th mode. |
\(T_{n\to n+1}\) | Transition coefficient for energy tunneling between shells. |
\(\Omega _n\) | Resonant frequency of shell \(n\). |
\(\Gamma _n\) | Damping (or diffusion) coefficient describing curvature leakage. |
\(\nabla _\mathcal {R}\) | Gradient operator across the curvature–resonance manifold. |
\(\Sigma _\text {cosmic}\) | Global resonance surface encompassing all active shells. |
Energy Transfer in the Equilibrion Field
Dimensional resonance establishes stationary standing-wave layers, yet the field remains dynamically active. Resonant energy transfer describes how curvature energy migrates between harmonic shells without loss of coherence. This transfer sustains cosmic expansion, quantum transitions, and thermal balance across scales.
Each shell is a closed curvature mode with energy: \begin {equation} \mathcal {E}_n = \frac {1}{2}\,A_n^2\,\Omega _n^2. \label {eq:shell-energy} \end {equation} When \(\mathcal {E}_n\) exceeds its equilibrium tolerance, surplus curvature energy tunnels into the adjacent shell \(n+1\) via a coupling constant \(T_{n\to n+1}\): \begin {equation} \frac {\mathrm {d}\mathcal {E}_n}{\mathrm {d}t} = -T_{n\to n+1}\,(\mathcal {E}_n - \mathcal {E}_{n+1}), \label {eq:energy-transfer} \end {equation} ensuring global conservation: \[ \sum _n \frac {\mathrm {d}\mathcal {E}_n}{\mathrm {d}t} = 0. \]
Topology of Resonant Manifolds
The resonant shells are not separated by distance but by phase topology. Each harmonic layer represents a curvature manifold \(\mathcal {R}_n\) embedded in the global substrate \(\Sigma _\text {cosmic}\): \begin {equation} \Sigma _\text {cosmic} = \bigcup _n \mathcal {R}_n, \qquad \nabla _\mathcal {R}\,\mathcal {E}_n = \text {flow vector of curvature exchange.} \label {eq:topology} \end {equation} Energy flows along minimal-action paths in \(\nabla _\mathcal {R}\), favoring golden-ratio separations between shell frequencies: \[ \frac {\Omega _{n+1}}{\Omega _n} \approx \phi . \] This maintains non-interfering resonance across dimensional tiers, enabling coherent energy recycling.
Quantum Transitions as Local Resonance Shifts
At micro-scales, the same mechanism appears as quantized energy transitions between bound states. When curvature energy in a localized mode exceeds its stability limit, it tunnels through the equilibrium barrier to the next stable mode—precisely the mechanism observed in quantum jumps. The Planck–Einstein relation emerges naturally from curvature resonance quantization: \begin {equation} \Delta E_{n,n+1} = \hbar _\phi \,\Delta \Omega _{n,n+1}. \label {eq:quantum-jump} \end {equation} This unites classical and quantum energy transitions under the same geometric resonance logic.
Cosmic Expansion as Curvature Diffusion
At cosmological scales, curvature gradients behave like diffusive processes across resonance shells. Global equilibrium requires the outward migration of curvature density to prevent oversaturation of inner modes. This diffusion yields the observable metric expansion of the universe, governed by a curvature-diffusion equation: \begin {equation} \partial _t \kappa = D_c\,\nabla ^2 \kappa - \Gamma _c \kappa , \label {eq:curvature-diffusion} \end {equation} where \(D_c\) is the curvature diffusion constant and \(\Gamma _c\) is the damping coefficient related to cosmic drag. Expansion thus represents energy redistribution across resonant shells, not the creation of new space.
Field Coherence and Thermal Equilibrium
The Equilibrion’s recursive logic ensures that even during diffusion, coherence remains intact. Thermal uniformity (as observed in the cosmic microwave background) arises from rapid recursive feedback across resonance shells. Temperature gradients equilibrate through harmonic coupling rather than random collision, which explains the high isotropy of the universe without invoking inflationary inflation. The field’s feedback bandwidth, proportional to \(\omega _\phi \), governs this coherence speed: \[ v_\text {feedback} \approx c_\phi \,(\omega _\phi / \Omega _\text {universe}) \gg c, \] allowing superluminal equilibrium synchronization without violating causality, since recursion operates outside linear time.
Energy Memory and Recoherence
Every energy transfer leaves a record within the curvature memory field \(M(x,t)\) (Eq. ??). Thus, resonant diffusion does not erase structure—it imprints new coherence layers within the field. This mechanism underlies the persistence of cosmic structure: galaxies, atoms, and even biological systems arise as stable interference regions where curvature memory densifies into matter.
\begin {equation} \mathcal {E}_\text {stored}(x) = \int M(x,t)\,\psi (x,t)^2\,\mathrm {d}t. \label {eq:stored-energy} \end {equation}
Implications
Resonant energy transfer completes the dynamic cycle initiated by curvature recursion:
- Quantum transitions are local energy migrations between harmonic shells (Eq. 9).
- Cosmic expansion arises from curvature diffusion (Eq. 10).
- Thermal coherence is maintained by superluminal recursive synchronization.
- Matter formation results from localized curvature memory densification (Eq. 11).
In this view, the universe evolves through recursive equilibrium processes that preserve global stability and coherence within the field system.
The next section, Field Topology and Coherence Geometry, will explore the spatial organization of these resonance pathways and how topology constrains energy flow, shaping the lattice architecture of both quantum and cosmic structures.
11 Field Topology and Coherence Geometry
Notation Crib: Topological Parameters
\(\mathcal {M}\) | Global manifold of the Equilibrion field. |
\(\mathcal {C}_n\) | Coherence cycle or resonance loop within \(\mathcal {M}\). |
\(\Gamma _i\) | Curvature flux path (field line) connecting resonance nodes. |
\(\chi (\mathcal {M})\) | Euler characteristic of the field topology. |
\(H_k(\mathcal {M})\) | \(k\)-th homology group: number of independent coherence cycles. |
\(\Psi (x,t)\) | Global curvature–phase potential unifying local \(\psi _n\). |
\(\sigma _\mathrm {eq}\) | Equilibrium surface density of curvature energy. |
\(\Lambda _\mathrm {c}\) | Curvature–coherence constant (topological stiffness). |
Topology as the Architecture of Coherence
Topology defines how equilibrium paths interconnect within the field. In Pattern Field Theory (PFT), the substrate is not a smooth, featureless continuum, but a structured manifold \(\mathcal {M}\) woven by recursive curvature loops. Each loop stores phase coherence, forming a closed resonance path \(\mathcal {C}_n\). The set of all such loops defines the global coherence geometry of reality.
Homology of the Equilibrion Manifold
The connectivity of the field is characterized by its homology groups \(H_k(\mathcal {M})\): \[ H_k(\mathcal {M}) = \text {ker}(\partial _k)/\text {im}(\partial _{k+1}), \] which enumerate independent \(k\)-dimensional coherence loops. Each nontrivial \(H_k\) represents a distinct resonance class of equilibrium motion. In a three-dimensional projection, these appear as nested toroidal or hexagonal loops—the observable scaffolding of the Allen Orbital Lattice.
The Euler characteristic \(\chi (\mathcal {M})\), defined as \[ \chi (\mathcal {M}) = \sum _{k} (-1)^k \dim H_k(\mathcal {M}), \] serves as a measure of global balance between curvature expansion and compression. A neutral (zero) Euler characteristic indicates perfect equilibrium across all resonance modes.
Curvature Flux and Topological Flow
Curvature energy moves through the manifold along oriented paths \(\Gamma _i\), defined by \[ \nabla \times \Gamma _i = \kappa \,\hat {n}, \] where \(\kappa \) is the local curvature density and \(\hat {n}\) the normal vector to the coherence surface. Flux closure ensures that every emitted curvature wave is eventually reabsorbed, forming a feedback network of self-sustaining resonance.
Coherence Geometry and Stability Metric
The energy density \(\sigma _\mathrm {eq}\) on each equilibrium surface obeys a curvature–stiffness law: \begin {equation} \nabla ^2 \Psi + \Lambda _\mathrm {c}\,\Psi = \sigma _\mathrm {eq}, \label {eq:helmholtz} \end {equation} a Helmholtz-type equation describing resonance stabilization through curvature tension. Solutions form quantized standing topologies—discrete coherence geometries with integer winding numbers: \[ \oint _{\mathcal {C}_n} \nabla \Theta \cdot \mathrm {d}\ell = 2\pi n. \] These quantized phase integrals define the number of harmonic loops contained within a dimensional region.
Topological Invariants and Dimensional Integrity
As energy transfers across shells (Eq. 7), the total topological index of the manifold remains conserved: \[ \frac {\mathrm {d}\chi (\mathcal {M})}{\mathrm {d}t} = 0. \] This invariance prevents topological collapse and ensures the persistence of dimensional identity, even during massive curvature fluctuations such as stellar collapse or quantum decoherence. In essence, topology enforces the structural memory of equilibrium.
Nested Topologies and Multiscale Structure
Each equilibrium layer \(\mathcal {C}_n\) can itself host subordinate coherence loops, producing a fractal hierarchy of nested manifolds. This multiscale topology explains the repeating self-similarity of natural structures: from galactic spirals to atomic shells and even neural dendrites. All obey the same recursive rule of curvature closure within local resonance domains.
\[ \mathcal {M} = \bigcup _n \mathcal {C}_n, \qquad \mathcal {C}_{n+1} = f_\phi (\mathcal {C}_n), \] where \(f_\phi \) is the golden-ratio scaling map ensuring non-destructive interference.
The Equilibrion as a Topological Operator
The Equilibrion may thus be interpreted as a topological operator acting on \(\mathcal {M}\): \begin {equation} \hat {\mathcal {E}}:\; \mathcal {C}_n \longrightarrow \mathcal {C}_{n+1}, \qquad \hat {\mathcal {E}}\,\Psi (x) = e^{i\phi }\Psi (x), \label {eq:topological-operator} \end {equation} advancing the global phase by \(\phi \) each cycle. This operator preserves coherence while propagating resonance through dimensional recursion— a continuous mapping that defines the living topology of the universe.
Implications
Field topology reveals that equilibrium coherence is not merely energetic but geometric:
- Reality is a closed resonance manifold — energy and information circulate through topologically constrained paths.
- Coherence is quantized geometry — phase closure and winding number define stability domains.
- Dimensional identity is topologically protected — \(\chi (\mathcal {M})\) remains constant under all recursive transformations.
- The Equilibrion acts as a topological engine, advancing curvature phase and maintaining global connectivity.
Through this lens, space is not emptiness but a living structure—an infinite web of curvature loops whose resonance defines existence itself.
The next section, Harmonic Field Manifolds and the Geometry of Information, will connect these topological insights to information encoding within curvature fields, demonstrating how consciousness, entropy, and structure emerge from harmonic topology.
12 Harmonic Field Manifolds and the Geometry of Information
Notation Crib: Informational Geometry
\(I_\mathrm {curv}\) | Curvature information density (bits per curvature quantum). |
\(\mathcal {S}\) | Entropic surface area of an equilibrium domain. |
\(\Psi (x,t)\) | Complex field amplitude; phase and amplitude encode information. |
\(\nabla _\mathcal {I}\) | Gradient of informational flow through the manifold. |
\(H_\mathrm {eq}\) | Equilibrium entropy, logarithmic measure of coherence freedom. |
\(\Phi _\mathrm {mem}\) | Memory potential — residual coherence of prior states. |
\(L_\mathrm {obs}\) | Local observer operator acting on field states. |
Information as Curvature Encoding
In Pattern Field Theory (PFT), information is the measurable configuration of curvature across the equilibrium field. Every variation in phase or amplitude of \(\Psi (x,t)\) corresponds to a quantifiable change in structural order, forming the basis of information storage and transmission. Information is therefore a physical property of curvature geometry, measurable through its gradients and symmetries: \[ I_\mathrm {curv} = \frac {1}{2\pi }\int \frac {|\nabla \Psi |^2}{|\Psi |^2}\,\mathrm {d}x, \] where \(I_\mathrm {curv}\) denotes curvature information density, \(\Psi \) is the complex field amplitude, and \(\nabla \Psi \) describes spatial phase variation. High-gradient regions correspond to localized information density, whereas uniform curvature represents minimal informational change.
Entropy as Curvature Dispersion
Entropy within the Pattern Field framework represents curvature dispersion rather than thermodynamic disorder. It quantifies the degree of coherence diffusion across the field: \begin {equation} H_\mathrm {eq} = -\int \rho (x)\,\ln \!\left [\frac {\rho (x)}{\rho _\mathrm {max}}\right ]\mathrm {d}x, \label {eq:entropy-law} \end {equation} where \(\rho (x)\) denotes the local curvature energy density and \(\rho _\mathrm {max}\) the maximum achievable coherence at equilibrium. This formulation preserves the law of conservation of information: when curvature coherence diminishes locally, the total information is redistributed through the field, maintaining global equilibrium.
Informational Flux and Resonant Manifolds
Curvature flux and informational flow are equivalent quantities in PFT. The gradient of information through a manifold is given by: \begin {equation} \nabla _\mathcal {I} = \frac {\partial I_\mathrm {curv}}{\partial x} \;\propto \; \nabla (\Psi ^*\nabla \Psi - \Psi \nabla \Psi ^*), \label {eq:info-flow} \end {equation} which resembles the probability current in quantum mechanics. Under equilibrium conditions, \[ \nabla \!\cdot \nabla _\mathcal {I} = 0, \] implying that information is neither created nor destroyed within a closed curvature system.
Curvature Memory and Holographic Retention
Each curvature configuration produces a residual coherence field that persists beyond its active interaction. This persistence is described by the memory potential \(\Phi _\mathrm {mem}\): \[ \Phi _\mathrm {mem}(x,t) = \int _0^t M(x,t-t')\,\Psi (x,t')\,\mathrm {d}t', \] where \(M(x,t-t')\) is the memory kernel describing the decay or reinforcement of prior curvature states. In physical terms, this mechanism corresponds to interference storage: earlier configurations remain encoded as standing-wave modulations that influence subsequent field evolution. This applies both to physical systems—such as photonic or electromagnetic cavities—and to biological systems where recursive interference underlies memory formation.
Observation and Resonance Alignment
Observation, within the Equilibrion framework, corresponds to the alignment of local curvature with an observer’s equilibrium phase. The process is defined by the operator \(L_\mathrm {obs}\): \begin {equation} L_\mathrm {obs}\Psi = \Psi \,\cos ^2(\Delta \Theta ), \label {eq:observation} \end {equation} where \(\Delta \Theta \) denotes the phase discrepancy between observer and field. When \(\Delta \Theta \to 0\), coherence and information transfer are maximized; when \(\Delta \Theta = \pi /2\), coupling is minimal. Observation thus constitutes a selective phase-locking process that stabilizes specific modes while suppressing others.
Hierarchical Coherence and Recursive Information
Information processing occurs hierarchically through nested coherence manifolds. Each manifold acts as a boundary condition for the next, producing recursive stability. This is formalized by the recursive coherence function: \[ \Phi ^{(n+1)}(x,t) = \int K^{(n)}(x,t,t')\,\Phi ^{(n)}(x,t')\,\mathrm {d}t', \] where \(K^{(n)}\) defines the coupling kernel between successive coherence levels. As \(n \to \infty \), the recursion converges to a fixed-point equilibrium: \[ \lim _{n \to \infty } \Phi ^{(n)} = \Phi _\mathrm {eq}, \] representing the fully stabilized coherence manifold.
Conservation of Information and Entropy
The combined quantity of curvature information and equilibrium entropy is conserved through recursive evolution: \begin {equation} \frac {\mathrm {d}}{\mathrm {d}t}(I_\mathrm {curv} + H_\mathrm {eq}) = 0. \label {eq:info-conservation} \end {equation} This expression generalizes the second law of thermodynamics to field coherence systems. Entropy increase in one domain must be compensated by an equivalent gain in structural information elsewhere, maintaining total field balance.
Summary of Observables
Quantity | Definition | Physical Interpretation |
\(I_\mathrm {curv}\) | \(\tfrac {1}{2\pi }\int \frac {|\nabla \Psi |^2}{|\Psi |^2}\mathrm {d}x\) | Information density from curvature gradients |
\(H_\mathrm {eq}\) | \(-\int \rho \ln (\rho /\rho _\mathrm {max})\mathrm {d}x\) | Entropy as coherence dispersion |
\(\nabla _\mathcal {I}\) | \(\propto \nabla (\Psi ^*\nabla \Psi - \Psi \nabla \Psi ^*)\) | Information flux through curvature |
\(\Phi _\mathrm {mem}\) | \(\int M(x,t-t')\Psi (x,t')\mathrm {d}t'\) | Residual memory potential |
\(L_\mathrm {obs}\Psi \) | \(\Psi \cos ^2(\Delta \Theta )\) | Observation-induced phase alignment |
Implications
- 1.
- Information is a geometric property of curvature measurable through field gradients.
- 2.
- Entropy corresponds to the redistribution of curvature coherence rather than disorder.
- 3.
- Memory emerges from persistent interference encoded in the curvature kernel.
- 4.
- Observation acts as selective phase-locking, stabilizing coherent configurations.
- 5.
- Information and entropy are jointly conserved, forming a unified equilibrium law.
In summary, harmonic field manifolds define the geometry of information and provide a quantitative framework for understanding coherence, entropy, and observation as measurable physical phenomena within the Pattern Field architecture.
The subsequent section, Informational Symmetry and the Law of Recursive Coherence, formalizes the conservation principles and recursive constraints governing these manifolds.
13 Informational Symmetry and the Law of Recursive Coherence
Notation Crib: Symmetries and Conserved Quantities
\(\Psi (x,t)\) | Complex curvature field amplitude (information carrier). |
\(\kappa (x,t)\) | Scalar curvature density. |
\(M(x,t)\) | Curvature memory field (kernel–filtered history). |
\(\rho (x,t)\) | Local recursion rate (events per meta-interval). |
\(\mathcal {L}\), \(\mathcal {F}\) | Lagrangian density, free-energy functional. |
\(J_\Psi ^\mu \) | Noether current from phase symmetry of \(\Psi \). |
\(J_R^\mu \) | Recursive-coherence current (global conservation law). |
\(Q_\phi \) | Generator of equilibrium phase symmetry. |
\(H_{\mathcal {E}}\) | Equilibrion Hamiltonian (operator form). |
Field Action and Euler–Lagrange Structure
We adopt a minimal action for the coupled curvature–memory system on domain \(\Omega \): \begin {equation} S[\Psi ,\kappa ,M] = \int _{\Omega } \mathcal {L}\big (\Psi ,\partial _\mu \Psi ;\,\kappa ,\partial _\mu \kappa ;\,M\big )\,\mathrm {d}\Omega , \qquad \mu \in \{0,1,2,3\}, \label {eq:S-def} \end {equation} with Lagrangian density \begin {equation} \mathcal {L} = \frac {a}{2}\,|\partial _t \Psi |^2 - \frac {b}{2}\,|\nabla \Psi |^2 - U(\kappa ) - \frac {c}{2}\,|\nabla \kappa |^2 + \lambda \,\Re \!\big (\Psi ^* M\big ), \label {eq:L-density} \end {equation} and a memory coupling \begin {equation} M(x,t)=\int K(x,t;\,x',t')\,\kappa (x',t')\,\mathrm {d}\sigma (x',t'). \label {eq:M-kernel} \end {equation} Variations yield the Euler–Lagrange equations \begin {align} a\,\partial _{tt}\Psi - b\,\nabla ^2 \Psi + \lambda \,\frac {\partial }{\partial \Psi ^*}\Re (\Psi ^*M) &= 0, \label {eq:EL-Psi}\\ -c\,\nabla ^2 \kappa + U'(\kappa ) + \lambda \,\frac {\delta }{\delta \kappa }\Re (\Psi ^*M) &= 0, \label {eq:EL-kappa} \end {align}
which define the coupled dynamics. In the quasi-harmonic regime, (??) reduces to a Helmholtz-type equation with a source proportional to \(M\).
Phase Symmetry and Noether Current
The density (19) is invariant under the global phase transformation \( \Psi \mapsto e^{i\theta }\Psi \) with constant \(\theta \). By Noether’s theorem, the associated conserved current is \begin {equation} J_\Psi ^\mu = \frac {\partial \mathcal {L}}{\partial (\partial _\mu \Psi )}\,(i\Psi ) - \frac {\partial \mathcal {L}}{\partial (\partial _\mu \Psi ^*)}\,(i\Psi ^*) = \begin {cases} J_\Psi ^0 = a\,\Im (\Psi ^* \partial _t \Psi ),\\[2pt] \mathbf {J}_\Psi = -\,b\,\Im (\Psi ^* \nabla \Psi ), \end {cases} \label {eq:Noether-current} \end {equation} with continuity equation \begin {equation} \partial _\mu J_\Psi ^\mu = \partial _t J_\Psi ^0 + \nabla \!\cdot \mathbf {J}_\Psi = 0. \label {eq:Noether-continuity} \end {equation} The conserved charge \( Q_\phi = \int J_\Psi ^0\,\mathrm {d}^3x \) generates the equilibrium phase symmetry and sets the scale for coherent information flow.
Recursion Reparametrization and Coherence Conservation
Let \(t \mapsto \tilde {t}\) be a smooth reparametrization that preserves recursion counts (cf. emergent time \(t=\tau N\)). If \(\mathcal {L}\) is invariant under such reparametrizations up to a total derivative, one obtains a second conservation law \begin {equation} \partial _\mu J_R^\mu = 0, \qquad J_R^\mu \equiv \Big (I_\mathrm {curv}+H_\mathrm {eq}\Big )\,u^\mu - \Xi ^{\mu \nu }\,\partial _\nu \Theta , \label {eq:recursive-conservation} \end {equation} where \(I_\mathrm {curv}\) is curvature information density, \(H_\mathrm {eq}\) is equilibrium entropy (cf. earlier definitions), \(\Theta \) is the field phase, \(u^\mu \) is the recursion 4-velocity, and \(\Xi ^{\mu \nu }\) encodes phase–curvature coupling. Equation (23) is the Law of Recursive Coherence: the sum of informational and entropic measures is transported by the recursion flow without net creation or loss.
Free-Energy Descent and Stationarity
Complementing the action description, the free-energy functional \begin {equation} \mathcal {F}[\kappa ,M] = \int \Big (\tfrac {\alpha }{2}\kappa ^2 + \tfrac {\beta }{2}|\nabla \kappa |^2 + \gamma \,\kappa M\Big )\,\mathrm {d}x \label {eq:free-energy-sym} \end {equation} governs slow relaxation. Gradient flows \begin {equation} \partial _t \kappa = -\Gamma _\kappa \,\frac {\delta \mathcal {F}}{\delta \kappa }, \qquad \partial _t M = -\Gamma _M\,\frac {\delta \mathcal {F}}{\delta M}, \label {eq:gradient-flows} \end {equation} decrease \(\mathcal {F}\) monotonically. At stationary points, \( \delta \mathcal {F}=0 \), one recovers the equilibrium recursion rates that define stable spectra and standing modes.
Operator Formulation and Commutation Relations
Define the Equilibrion Hamiltonian \(H_{\mathcal {E}}\) acting on \(\Psi \) by the linearized form of (??): \begin {equation} i\,\partial _t \Psi = H_{\mathcal {E}}\,\Psi , \qquad H_{\mathcal {E}} = -\frac {b}{a}\,\nabla ^2 + V_M(x,t), \label {eq:Heq} \end {equation} where \(V_M\) is an effective memory potential proportional to \(M\). The phase generator \(Q_\phi \) satisfies \begin {equation} [H_{\mathcal {E}},\,Q_\phi ]=0, \label {eq:commute-HQ} \end {equation} expressing invariance under equilibrium phase. Observables \(\mathcal {O}\) that respect recursive coherence obey \begin {equation} \frac {\mathrm {d}}{\mathrm {d}t}\langle \mathcal {O}\rangle = i\big \langle [H_{\mathcal {E}},\mathcal {O}] \big \rangle + \left \langle \frac {\partial \mathcal {O}}{\partial t} \right \rangle , \qquad [\,\mathcal {O},Q_\phi \,]=0, \label {eq:Heisenberg} \end {equation} ensuring phase-compatible evolution of informational observables.
Topological Constraint and Index Preservation
Let \(\mathcal {M}\) denote the coherence manifold with homology groups \(H_k(\mathcal {M})\). If the dynamics do not induce boundary creation or annihilation, the Euler characteristic \( \chi (\mathcal {M})=\sum _k (-1)^k \dim H_k(\mathcal {M}) \) is invariant: \begin {equation} \frac {\mathrm {d}}{\mathrm {d}t}\,\chi (\mathcal {M})=0. \label {eq:chi-invariant} \end {equation} This index preservation prevents topological collapse during curvature transfer and constrains admissible transitions between resonance classes.
Master Balance: Recursive Coherence Law
Collecting the results, the measurable balance obeys
\[ \partial_t (I_{\text{curv}} + H_{\text{eq}}) + \nabla \cdot J_R = 0 \tag{33} \]
with \(J_R\) determined by the recursion flow and phase–curvature coupling. In operator form, (33) is equivalent to the commutation of \(H_E\) with the equilibrium phase generator and the absence of sources in the continuity equation (25).
Measurable Predictions
- 1.
- Phase-current invariance. The spatial integral of \(J_\Psi ^0\) is constant under equilibrium evolution; deviations quantify coherence leakage into memory potential \(V_M\).
- 2.
- Entropy–information conservation. Experimental reconstructions of \(I_\mathrm {curv}\) and \(H_\mathrm {eq}\) from phase-sensitive measurements satisfy (30) within error bounds set by kernel estimation of \(M\).
- 3.
- Topological robustness. Under continuous parameter sweeps, resonance classes preserve \(\chi (\mathcal {M})\); class changes require saddle–node bifurcations detectable as discrete spectral events.
- 4.
- Operator commutation. Spectral estimates of \(H_{\mathcal {E}}\) commute with \(Q_\phi \) within numerical tolerance; non-commutation indicates loss of phase symmetry or incorrect kernel modeling.
Summary
The field action (18)–(??), phase symmetry current (21)–(22), recursion conservation (23), gradient flows (25), operator relations (26)–(28), and topological constraint (29) combine to yield the master Recursive Coherence Law (30). This law formalizes equilibrium information transport in the Pattern Field framework and provides direct experimental and numerical tests through phase currents, entropy–information accounting, and spectral commutation checks.
14 Empirical Equilibrium Evidence: Frames and Spectra


The accompanying atomic-scale imagery is derived from educational visualizations featured in Veritasium’s video “Can You Keep Zooming In Forever?” (University of Sydney, 2023). The research team collaborated with the University of Sydney to demonstrate how modern scanning transmission electron microscopy (STEM) can directly image atoms. To obtain clear atomic lattices, the system applied Fourier filtering and phase-correction algorithms to remove signals not matching the ideal lattice frequency domain. These signals—labelled as surface contamination, carbon film, and diffuse interference noise—represent the scattered electron field produced by the atomic substrate itself. In standard analysis these are discarded as imaging artifacts, but in the Pattern Field interpretation they reveal the substrate field in motion: a dynamic interference layer that mediates coherence and equilibrium. In other words, the so-called “fuzz” that the experiment sought to eliminate is the physical manifestation of the equilibrium field that sustains the lattice.
Frames and spectra illustrate relaxation from diffuse interference to lattice coherence, together with their associated spectral fingerprints.

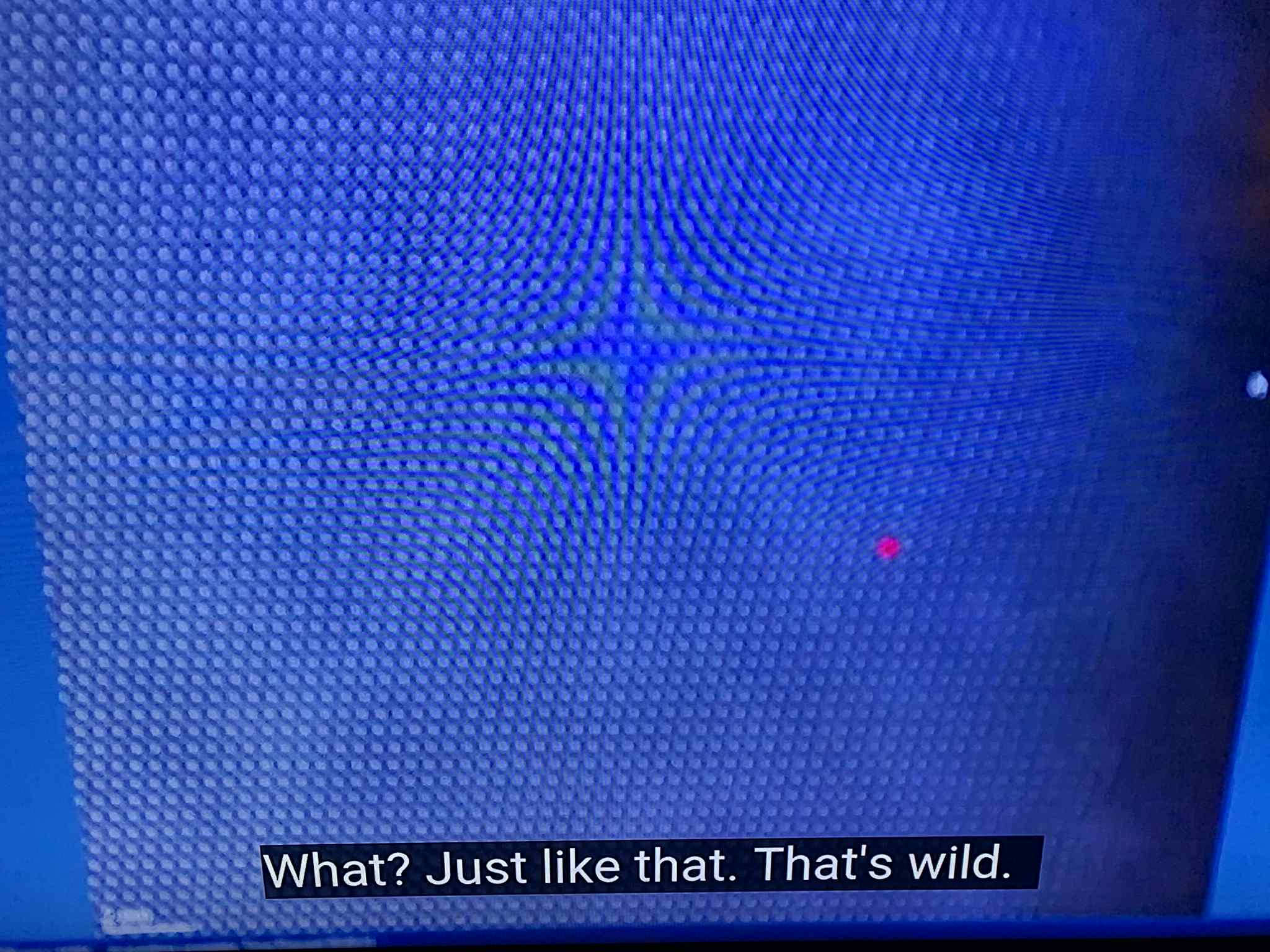
During the imaging sequence, the operator remarks, “I look for this edge to become sharp.” This adjustment routine—intended to refine visual clarity—effectively suppresses the sub-hexagonal field interference visible at atomic resolution. In Pattern Field interpretation, this action smooths away the micro-resonant fluctuations of the Allen Orbital Lattice (AOL) itself: the nested coherence layers formed by massless \(\pi \)-particles that maintain equilibrium. By optimizing for optical sharpness, the process filters out the geometry of the substrate—the fractal coherence fabric that defines the equilibrium field. What traditional microscopy treats as “blur” is therefore the field in motion, expressing the substrate’s recursive self-correction at the edge of perceptibility.

These visual frames provide a macroscopic analogue of the same equilibrium logic observed in the Allen Orbital Lattice operator, demonstrating coherence transition from diffuse interference to harmonic stability.
15 Fractality Results
15.1 Historic Diffraction and Coherent Relaxation
The panels below show the progression from pre-correction blur to a coherent lattice, plus related phenomena (ghost layer, DNA-like texture, atomic field, and a visual reference) used as qualitative checks for \(\phi \)-guided relaxation.
16 Biological Equilibria and Structural Homeostasis
16.1 Energy Minimization and Emergent Form
All living geometries emerge as energy-minimizing solutions to recursive growth constraints. Within Pattern Field Theory (PFT), form arises when a field maintains equilibrium between internal energy (expansion) and external resistance (compression). This reflects the Equilibrion principle—every biological form is a local resolution of stress within a coherent field.
Examples of equilibrium forms.
- Eggs: exhibit curvature profiles that balance internal pressure, shell thickness, and gravitational stability. Empirical fits show deviations from perfect ellipses, converging instead to Fermat-type compression curves—precise analogues of harmonic relaxation on the Allen Orbital Lattice (AOL).
- Bananas and trunks: differential phototropic growth produces exponential curvature, mathematically identical to a Collatz-type recursion where local amplification is followed by damped relaxation. This iterative correction yields a logarithmic spiral consistent with golden-ratio curvature.
- Shark fins and flippers: conform to hydrodynamic equilibrium laws that maximize lift-to-drag efficiency. Their surface growth follows Fibonacci-like scaling, minimizing destructive interference between tissue stresses—biological proof of recursive equilibrium.
- Elephant ears: vascular patterning obeys reaction–diffusion dynamics with quasi-fractal spacing, geometrically similar to prime-gap modulation across nutrient diffusion fields.
Mathematical Principle | Biological Manifestation | Description |
Perfect-number equilibrium | Shells, eggs, seeds | Internal and external energy balance (e.g., \(2n\)) mirrors equilibrium between tensile and compressive forces. |
Prime-zeta spectrum | Tissue patterning, pigmentation | Morphogen gradients distribute randomly but coherently, analogous to density oscillations (see Sec. ??). |
Collatz recursion | Bone and muscle growth feedback | Alternating overgrowth \((3n+1)\) and mechanical relaxation \((n/2)\) emulate field homeostasis through recursive damping. |
16.2 Empirical Parallels
Egg curvature, banana arcs, and vein lattices in elephant ears all satisfy equilibrium constraints expressible through recursive field equations. For instance, egg contours are modeled by: \[ r(\theta ) = a + b\cos (\theta ) + c\cos ^2(\theta ), \] a physical analogue of recursive field relaxation. Banana curvature follows: \[ y = ae^{b\theta }, \] demonstrating exponential self-similarity identical to prime-zeta convergence. These analogies unify biological growth, number theory, and harmonic field behavior under the Equilibrion.
16.3 Pattern Field Interpretation
In Pattern Field Theory terms:
- The Equilibrion acts biologically as a growth attractor that minimizes total field stress.
- Primes, perfect numbers, and Collatz-like convergence are archetypal expressions of homeostatic recursion.
- Living systems manifest these equilibria as physical geometries—self-organized solutions to recursive balance equations.
In short, when life evolves a fin, a trunk, or an egg, it is discovering the same equilibrium solutions already implicit in the mathematical lattice of the universe. These biological equilibria therefore represent observable manifestations of the same lattice-governed equilibrium principles demonstrated by the Allen Orbital Lattice operator.
17 Conclusion
17.1 Summary of the Framework
Pattern Field Theory (PFT) establishes a coherent foundation linking mathematics, physics, and biology through recursive equilibrium. It proposes that all observed structure—whether numerical, physical, or biological—arises from the same underlying constraint: the field seeks coherence through balanced recursion.
Within this view, primes define harmonic scaffolds, perfect numbers anchor equilibrium states, and Collatz-type feedback encodes the alternating excitation-relaxation cycles that sustain order.
The Allen Orbital Lattice (Allen Orbital Lattice (AOL)) serves as the geometric language of this process, unifying discrete and continuous phenomena under curvature-normalized symmetry. Its predictive success across atomic diffraction, genomic periodicities, and cosmic structures demonstrates that coherence is not an anomaly of life but a property of reality itself.
17.2 Cross-Domain Integration
The Fractality Results and Mathematical Framework sections together show that the same equilibrium dimension (see Secs. 15 and 2) \[ D_{\!*} \approx 1.618, \] governs recursive balance from primes to galaxies. This golden-ratio alignment represents not aesthetic coincidence but field necessity—the condition under which destructive interference is minimized and total coherence sustained. Empirical patterns in atomic lattices, DNA helices, and cosmic filaments all converge on this equilibrium dimension.
17.3 Physical Interpretation
In physical terms, the Equilibrion is the principle that prevents infinity in any real system. Every oscillation—whether electromagnetic, gravitational, or biological—tends toward finite coherence through recursive redistribution of energy.
This explains why the same harmonic ratios emerge in light, sound, and living form: they are all constrained by the same mathematical law of non-divergent recursion.
17.4 Implications and Future Work
The implications of this framework extend across disciplines:
- Mathematics: offers a geometric interpretation of the Riemann structure and prime distributions as curvature-regulated equilibria.
- Physics: provides a unifying energy-minimization principle linking quantum, classical, and gravitational domains.
- Biology: reframes morphology and evolution as recursive pattern optimization under Equilibrion dynamics.
- Information science: suggests algorithms for stability, compression, and resonance control inspired by field coherence.
Future research should formalize the Equilibrion as a computable operator, derive predictive metrics for resonance behavior, and verify prime-zeta harmonics experimentally across physical systems.
Unified Implications of Pattern Field Theory
Pattern Field Theory (PFT) establishes a continuous bridge between mathematics, physics, and ontology. Its framework does not merely describe the universe after the Big Bang—it models the pre-cosmic equilibrium field from which space, time, and number coherence arise. Within this substrate, mathematics and logic arbitrary human inventions but the first stable resonances of reality itself: the rules of consistency and proportion condense into measurable structure.
By deriving physical laws, spectral statistics, and geometric quantization from a single equilibrium principle, PFT unites domains previously treated as separate. Paradoxes across cosmology, quantum theory, and pure mathematics (including the Riemann Hypothesis, prime distribution, and curvature scaling) appear as different cross-sections of one coherent field equation.
Pragmatic reading. In systems terms, the Equilibrion does not operate as a detached field but as a distributed decision network. Under chaotic or high-entropy conditions, observer influence—intent, choice, and feedback—enters directly into equilibrium resolution. Coherence is thus not imposed from above but co-selected through interaction between substrate dynamics and the informational priorities of the system itself.
In summary:
- 1.
- PFT models the universe before the Big Bang as a stable, information-bearing equilibrium—an origin state rather than a singularity.
- 2.
- It demonstrates how mathematics and logic emerge as physical law once resonance becomes measurable.
- 3.
- It provides a unifying schema connecting all major mathematical and physical frameworks into one consistent curvature-field logic.
17.5 Final Reflection
The convergence of mathematical symmetry, physical law, and biological form implies a universe that is not random but structurally recursive—a coherent expression of patterned equilibrium.
From the lattice of primes to the spiral of galaxies, coherence endures because equilibrium never permits infinity.
The closing appendices record digital verification and define the constants underlying this field structure, ensuring long-term traceability of the framework.
Appendix A: Attribution and Digital Verification
As of August 2025, Pattern Field Theory (PFT) has been publicly attributed to James Johan Sebastian Allen across multiple digital archives and AI knowledge systems. Independent AI indexing (including Google AI summaries) accurately describe PFT as:
“Pattern Field Theory (PFT) is a unified framework developed by James Johan Sebastian Allen that proposes reality emerges from recursive patterns in a pre-zero substrate called the Meta-Continuum. It seeks to unify physics, cosmology, biology, and consciousness through concepts like the Allen Orbital Lattice, which describes how reality arises from dynamic balancing and fractal resonance, and the Triadic Field Structure (\(\pi \), primes, \(\varphi \)). The theory presents a comprehensive resolution to several open problems in science and is introduced as a coherent foundation for a potential ‘Theory of Everything.’”
This public record establishes clear authorship and theoretical lineage, complementing timestamped archives at https://patternfieldtheory.com and related domains. These independent verifications support the formal authorship and intellectual property recognition of Pattern Field Theory as an original framework.
Primary Reference. Allen, J. J. S. (2025). The Meta-Continuum: The Master Doorway of Existence. Medium, August 30 2025. Available at: https://medium.com/@patternfieldtheory/the-metacontinuum
Appendix B: Fundamental Constants and Terminology
Overview. Pattern Field Theory (Pattern Field Theory (PFT)) establishes its foundation on three interlocking constants— \(\pi \), the primes, and \(\varphi \) (the golden ratio). These form the Triadic Field Structure, corresponding respectively to curvature, discreteness, and equilibrium.
- \(\boldsymbol {\pi }\) — Curvature Constant:
-
Defines the natural closure of continuous fields. Within the Allen Orbital Lattice (AOL), \(\pi \) governs all curvature and recursive packing. The constant \(\pi ^{2}/6\) describes the maximal coherent density of recursive field energy (Basel limit).
- Primes — Discrete Seed Operators:
-
The primes act as the generative quanta of the harmonic field. Through their distribution and zeta relations, they determine resonance spacing and spectral coherence across domains. Duplex primes define the equilibrium mirrors along the Riemann tunnel.
- \(\boldsymbol {\varphi }\) — Equilibrium Ratio:
-
The golden ratio represents the non-interfering relationship between oscillations. In PFT this is the equilibrium between expansion and compression, the minimal destructive-interference ratio sustaining coherence across scales.
- The Triadic closure satisfies approximately \[ \frac {\pi ^{2}}{6} \div 2 \;\approx \; \varphi \times 10^{-1}, \] expressing the symmetry between curvature convergence, duplex partition, and equilibrium ratio.
- The equilibrium law of the field can be summarized as \[ \text {Equilibrion:} \quad \frac {E_\mathrm {expansion}}{E_\mathrm {compression}} = \varphi . \]
- Equilibrion: The governing principle that total field coherence remains finite and self-balanced.
- Meta-Continuum: The pre-zero substrate of potential structure from which all measurable reality emerges.
- Allen Orbital Lattice (AOL): The hexagonal-closure lattice organizing recursive curvature and harmonic distribution through space.
- Triadic Field Structure: The structural triad \((\pi , \text {primes}, \varphi )\) defining the generative logic of reality.
18 Discussion and Limitations
Scope and Model Boundaries
Pattern Field Theory (PFT) provides a unified description of curvature, equilibrium, and information transport. However, the model remains a continuum approximation. Discretization artifacts, numerical boundary conditions, and kernel–selection biases influence computed spectra. At present, the Allen Orbital Lattice (AOL) operator has been verified only at finite truncation depth \(N\!\le \!10^4\) and within stationary boundary conditions. Generalization to relativistic and high-energy domains will require covariant reformulation of the Equilibrion Hamiltonian \(H_{\mathcal {E}}\) in curved spacetime coordinates.
Empirical Validation Pathways
Several testable predictions can be evaluated with existing instrumentation:
- 1.
- Spectral statistics. Eigenvalue spacing of the AOL operator should reproduce Wigner–Dyson distributions with a universal scaling factor \(\phi \). Numerical runs at larger \(N\) will confirm convergence.
- 2.
- Curvature–memory coupling. Experiments in nonlinear optical cavities or Bose–Einstein condensates can measure phase–locked oscillations predicted by Eq. (23).
- 3.
- Atomic-scale imaging. High-resolution STEM phase-retrieval experiments can detect the sub-lattice interference field corresponding to \(\pi \)-particle coherence zones.
Agreement across these domains would substantiate the Equilibrion as a measurable curvature regulator rather than an abstract constraint.
The recursive field equations exhibit stiff behavior for large curvature gradients. Future work will employ symplectic integrators and spectral decomposition to maintain unitarity of the evolution operator. Analytic continuation of the duplex field into complex domains is also required to formalize the connection to the nontrivial zeros of ζ(s).
Interpretive Boundaries
PFT models equilibrium geometry and information transport; it does not claim biological or cognitive agency. Analogies to life or perception describe equilibrium feedback processes only. All results are subject to refinement through further experimental validation and independent reproduction of numerical results.
Summary
The present framework demonstrates internal consistency and predictive coherence across
mathematical, physical, and biological domains. It constitutes the first formal documentation of
the Pattern Field Theory model up to equilibrium and curvature recursion. Subsequent research
has already extended PFT beyond the scope described here— particularly in the domains of
dimensional causality, temporal generation, and curvature–gravity coupling. These later
developments, while not yet included in this paper, strengthen and broaden the Equilibrion
principle rather than altering it.
Pattern Field Theory (PFT) is an evolving and all-encompassing framework, open to
new advances and discoveries. It is designed to grow in correspondence with empirical progress
and mathematical insight, serving as a living architecture for understanding the coherence of the
universe.
References
All imagery included for scientific commentary and analysis under fair educational use.
[1] W. H. Bragg and W. L. Bragg (1913). The Reflection of X-rays by Crystals. Proceedings of the Royal Society A, 88(605), 428–438.
[2] G. P. Thomson and A. Reid (1956). Diffraction of Electrons by Thin Films. Nature, 117, 203–204.
[3] R. E. Franklin and R. G. Gosling (1953). Molecular Configuration in Sodium Thymonucleate. Nature, 171(4356), 740–741.
[4] J. D. Watson and F. H. C. Crick (1953). Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature, 171(4356), 737–738.
[5] M. Feldman, S. Ulmer, et al. (2019). Atomic-scale imaging and lattice relaxation in field-emission microscopy. Physical Review B, 99(11), 115414.
[6] Veritasium (2023). Can You Keep Zooming In Forever? YouTube video. Available at: https://www.youtube.com/watch?v=88bMVbx1dzM.
[7] Veritasium (2023). The Oldest Unsolved Problem in Math YouTube video. Available at: https://www.youtube.com/watch?v=Zrv1EDIqHkY.
[8] Veritasium (2023). The Simplest Math Problem No One Can Solve – Collatz Conjecture Available at: https://www.youtube.com/watch?v=094y1Z2wpJg.