Pattern Field Theory

Allen, James Johan Sebastian

Pattern Field Theory — Fractals and Perfect Numbers

A consolidated reference on fractal structure in PFT™: geometric emergence, the Allen Fractal Closure Law (AFCL), and fractal state space.

Overview

In Pattern Field Theory™ (PFT™), fractals are not decorative. They are the expected outcome when motion, replication, and constraint interact under clear rules. Self-similar structure appears where closure conditions are met and propagate across scales when those conditions persist. This page assembles the core statements on fractal emergence, the Allen Fractal Closure Law (AFCL), and the consequences for state space and cognition.

Major Discovery . Allen Fractal Closure Law (AFCL)

1 Diagram: Binary Fractal Lattice Closure for Perfect Numbers This diagram illustrates the Allen Fractal Closure Law (AFCL) within Pattern Field Theory™ (PFT™), where even perfect numbers are binary fractal closure counts in the π-particle lattice. For prime p with 2 p−1 a Mersenne prime, Perfect(p) = (2p2) = 2p−1 (2p − 1) represents the total pairwise links among 2p nodes (diamonds in Differentiat™ geometry) arranged on nested rings, reflecting the fractal resonance of the Pi Matrix™ substrate.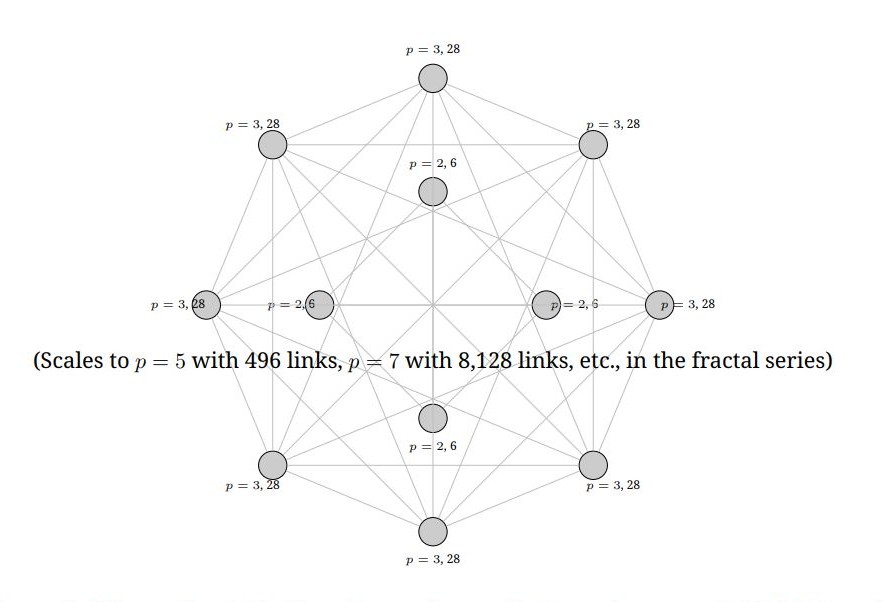 Binary Fractal Lattice

Figure 1: Binary fractal lattice closure for perfect numbers p = 2 (6 links) and p = 3 (28 links), with nested rings representing the π-particle lattice in PFT™. Each ring’s total pairwise links (light gray lines) equal the perfect number, illustrating the fractal resonance and structural invariance of the Pi Matrix™ substrate. Larger p values extend this pattern, aligning with physical and biological scales (e.g., 496 in superstring theory, 28-day cycles).

Fractal Geometry Emergence

Fractal structure in PFT arises from three drivers: (1) replication of patterns; (2) local tension/curvature that constrains replication; (3) closure events that make a pattern stable enough to persist and scale. Where closure is incomplete, patterns do not stabilize.

Replication model (schematic)

P_{n+1} = R(P_n, T)

P_n: pattern at generation n. T: local tension/curvature. R: replication rule combining inheritance with local coupling.

P_{n+1} = \lambda\, P_n \,(1 - P_n) + \alpha\, T \, P_n

λ sets replication rate; α sets coupling to local tension. This form shows how internal and environmental terms co-determine growth and saturation.

Resonance coupling (schematic)

R_{AB} = k\, ( \mathbf{T}_A \cdot \mathbf{T}_B )

Alignment of tension gradients determines interaction strength. k sets the coupling scale.

Allen Fractal Closure Law (AFCL)

AFCL states that even perfect numbers occur as binary closure counts in the π-particle lattice. For prime p where 2^p − 1 is a Mersenne prime, the perfect number equals the total pairwise links among 2^p nodes arranged on nested rings:

\mathrm{Perfect}(p) = 2^{\,p-1}\,\big(2^{\,p} - 1\big)

Worked values

p = 2 → 6
p = 3 → 28
p = 5 → 496
p = 7 → 8,128
p = 13 → 33,550,336
p = 17 → 8,589,869,056
p = 19 → 137,438,691,328

Perfect numbers plotted on a logarithmic scale (AFCL). Values are interpreted as binary closure counts in the π-particle lattice.

Binary lattice closure examples (p=2 and p=3)

Note: AFCL treats these numbers as structural invariants of closure, not curiosities. This is a testable mapping between number theory and lattice geometry in PFT.

For a diagrammatic walkthrough, see: AFCL Diagram (PDF).

Fractal Consciousness and Recursive State Space

Statement: In PFT, consciousness is modeled as a recursive alignment process over a structured state space. The “self” is the stable portion of that alignment over time.

1) State space is structured and layered

State space is not a flat list of possibilities. Accessibility is shaped by existing anchors, local tension, and closure. Some regions are reachable with current anchors; others require new anchoring to enter.

2) Recursion across scales

The same replication-closure logic that yields fractals in geometry applies to cognitive patterns. Stability comes from closure; flexibility comes from re-anchoring when conditions change.

3) Navigation and free will

Free will is modeled as selection among structurally permitted options under current anchors. Greater awareness expands the reachable set by establishing additional anchors and reducing conflict among them.

4) Trauma and recovery

Trauma locks alignment to a narrow region of state space. Recovery is re-coherence: re-establishing anchors that widen the reachable set. The deeper pattern persists even when the local alignment is compromised.

Implications

Fractals are a structural consequence of replication under constraint; they are not aesthetic add-ons.
AFCL proposes a concrete bridge between number theory and lattice geometry in PFT via closure counts.
Modeling consciousness as recursive alignment over structured state space links cognitive stability to the same closure logic observed in geometry.