The Taxonomy of Coherence Domains in Pattern Field Theory

From the Metacontinuum to Fractal Window Zones (FWZs): a rigorous, readable map of how coherence organizes the universe.

Scope. This article formalizes the coherence taxonomy in Pattern Field Theory (PFT), integrating the Metacontinuum as Unbound Fractality, the emergence of the Differentiat, the Pi Particle (π-particle), formation of the Allen Orbital Lattice (AOL), and the roles of the Equilibrion (EQB), Fractal Window Zones (FWZs), and multiple coherence domain classes. Acronyms are expanded on first use and restated where helpful.

Documentation Rule: Expanded Acronyms

Rule. Expand all acronyms on first use and restate them periodically in longer sections. Examples used here: Pattern Field Theory (PFT), Allen Orbital Lattice (AOL), Fractal Window Zone (FWZ), Semi-Permeable Coherence Domain (SPCD), Rigidly Static Coherence Domain (RSCD), Equilibrion (EQB).

Ontological Sequence of Emergence

  1. Metacontinuum — Unbound Fractality (logical origin).

    Unbound Fractality is a pre-ontological state in which logical and relational potential exists without boundary conditions, metric, or scale limitation. It is an infinitely recursive logical continuum—self-referential yet ontologically unresolved. Denote this domain by \( \mathcal{F}_\infty \). There is no terminal element, topology, or closure; only potential mappings that subdivide without limit.

  2. Differentiat — first bounded distinction.

    The initial act of differentiation (A ≠ B) partially constrains Unbound Fractality, introducing minimal boundary coherence. The Differentiat is pure relational distinction, not yet temporal; it is the first ontological reduction from infinite potential to finite identity.

  3. Pi Particle (π-particle) — first stable fractal coherence (fixed point).

    The Pi Particle (π-particle) is the first stable fractal within Pattern Field Theory (PFT): a massless structural invariant and self-consistent frequency state that functions as the minimal non-trivial fixed point of the Allen Orbital Lattice (AOL) renormalization operator (formally, \( \mathcal{R}(\psi_\pi)=\psi_\pi \)). It does not emit frequency; it embodies an intrinsic field parameter \( f_\pi = 1/T_\pi \). By defining local curvature and phase alignment over the minimal coherence domain, the π-particle establishes the first bounded lattice of logical stability and serves as the generative fractal kernel for all subsequent particles.

  4. Allen Orbital Lattice (AOL) — spatial coherence scaffold.

    A hexagonally organized network arising from consistent π-particle relations. The AOL does not sit in space; it constitutes space as relational continuity across nodes (stable alignments) and edges (coherence transfer paths).

  5. Equilibrion (EQB) — dynamic balancer.

    Regulates coherence densities across the lattice, preventing runaway divergence or collapse. Empirically, this presents as conservation-like regularities and homeostatic behavior across scales.

  6. Instantiated reality layers and time.

    Higher-order embeddings of resonance create particles, fields, and regions. Time emerges as the indexing of coherence updates within bounded domains; “universal time” is a statistical synchronization across many windows.

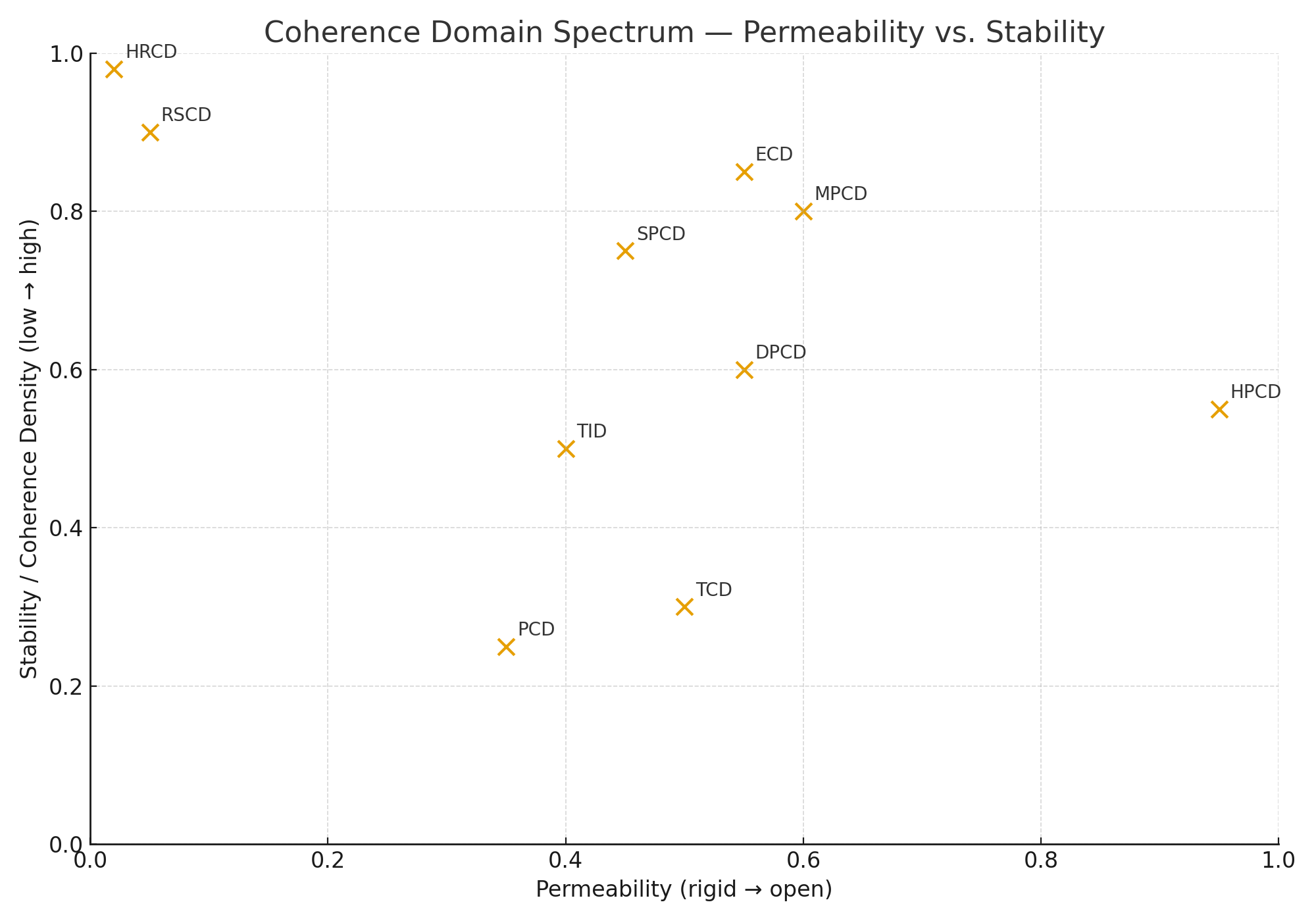
Coherence Domain Spectrum across permeability and stability axes
Figure X. Coherence Domain Spectrum — Understanding the taxonomy of coherence domains in Pattern Field Theory (PFT).

The chart shows how different kinds of systems organize themselves depending on two key properties:
  • Horizontal axis: Boundary permeability — how easily a system exchanges information or energy with its surroundings, from completely closed (left) to highly open (right).
  • Vertical axis: Stability or coherence density — how consistent and self-maintaining the system is, from unstable or short-lived (bottom) to stable and enduring (top).

Domains and their meanings:

RSCD – Rigidly Static Coherence DomainCompletely closed and highly stable; examples include crystalline or frozen structures. Anchors the left–upper corner (low permeability, high stability).
HRCD – Hyper-Rigid Coherence DomainTopologically sealed, self-referential domains; theoretically timeless invariants. Positioned at the extreme of rigidity.
SPCD – Semi-Permeable Coherence DomainSelectively open; allows limited exchange while maintaining form. Biological cells or individual minds fit here — moderately open yet organized.
DPCD – Dynamically Permeable Coherence DomainBoundaries open and close in rhythmic cycles. Think of heartbeats, breathing systems, or ecosystems that change seasonally.
MPCD – Meta-Permeable Coherence DomainComposed of nested sub-domains; coordinates many smaller systems. Represents organisms, organizations, or planetary biospheres.
ECD – Equilibrial Coherence DomainLong-term balanced systems maintaining homeostasis. Found near the spectrum center, where exchange and stability are equal.
HPCD – Hyper-Permeable Coherence DomainExtremely open, almost fully transparent boundaries; information flows freely. Comparable to collective or entangled fields.
TCD – Transient Coherence DomainShort-lived events; structures that appear briefly and dissolve. Found near the bottom of the diagram, with low stability.
PCD – Proto-Coherence DomainDiffuse pre-organized regions such as plasmas or turbulence. Low stability and weakly defined boundaries.
TID – Transitional Interface DomainBoundary layers connecting other domains; act as bridges for information exchange.

Together these domains trace a full continuum—from rigidly static structures through adaptive, living systems to fluid, collective states—mapping how coherence evolves as boundaries open and stability adjusts.

Coherence (ontological definition)

Coherence is the minimal condition under which a series of relational events maintain internal consistency and reproducibility across recursive iterations. Let \( \Phi(r_i,r_j) \) denote a relational phase/logic mapping between events \( r_i, r_j \). Coherence holds when \[ \forall (r_i,r_j),\quad \Delta\Phi(r_i,r_j) < \varepsilon_c, \] where \( \varepsilon_c \) is the domain’s coherence threshold.

Law of Semi-Permeable Coherence Domains (SPCDs)

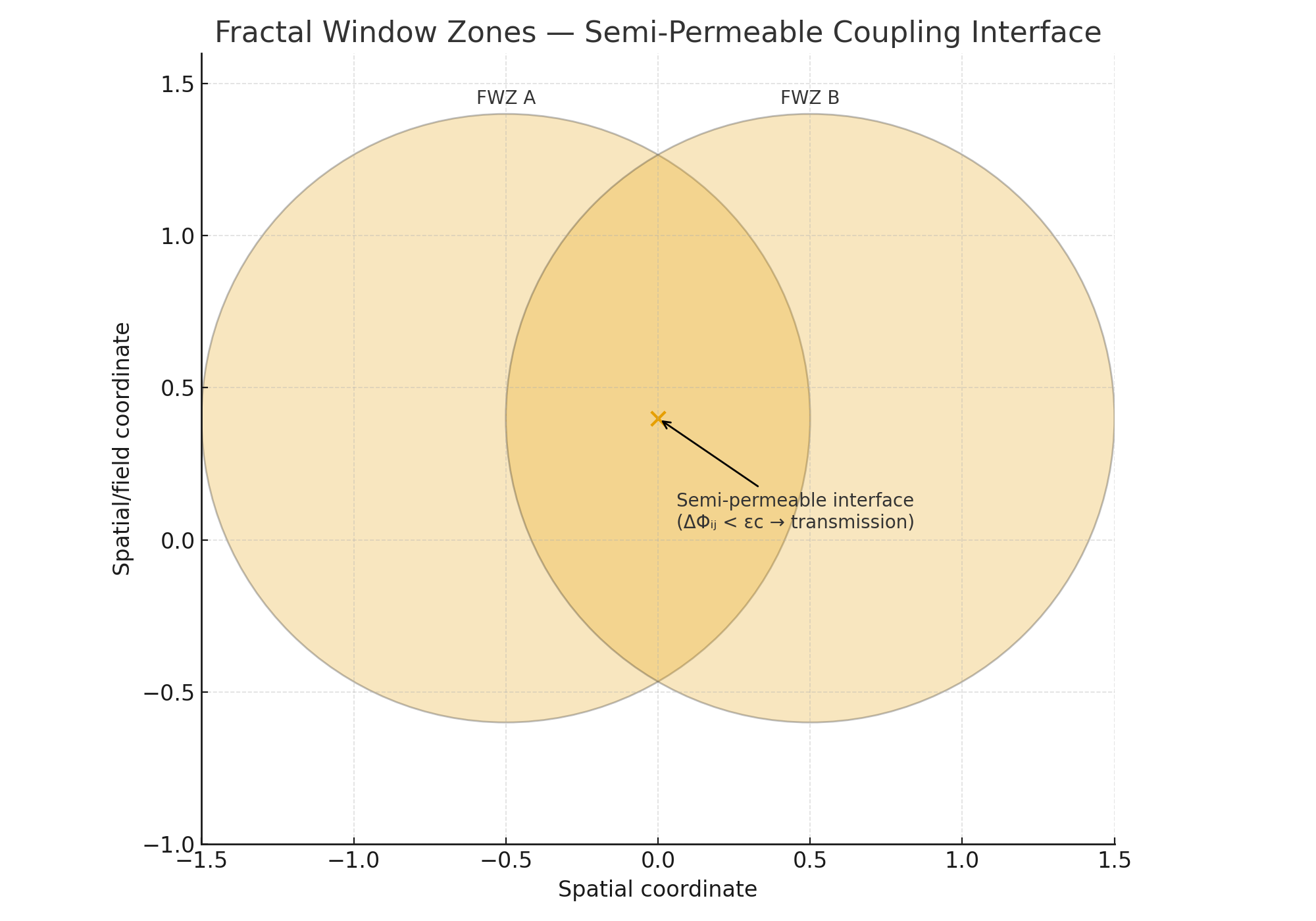
Two overlapping Fractal Window Zones with a semi-permeable interface
Fractal Window Zones (FWZs) — semi-permeable coupling. A channel forms in the overlap when the phase discrepancy satisfies ΔΦij < εc, enabling coherence exchange (per the Law of Semi-Permeable Coherence Domains).

Statement. Every Fractal Window Zone (FWZ) operates as a Semi-Permeable Coherence Domain (SPCD), selectively exchanging pattern information with adjacent domains according to coherence compatibility. If windows \( \mathcal{W}_i \) and \( \mathcal{W}_j \) exhibit phase discrepancy \( \Delta\Phi_{ij} \) below tolerance \( \varepsilon_c \), a transmission channel exists.

Interaction integral: \[ I_{ij} = T_{ij} \int_{\partial \mathcal{W}_i \cap \partial \mathcal{W}_j} \Psi_i^{*}\,\Psi_j\, dA,\quad T_{ij} \in [0,1], \] where \( \Psi_k \) are local coherence states and \( T_{ij} \) is the permeability function.

Inter-Window Communication and Pattern Interaction

Communication is coherence exchange across semi-permeable boundaries: a structural synchronization rather than symbolic transmission alone. A channel \( \Gamma_{ij}:\mathcal{W}_i \leftrightarrow \mathcal{W}_j \) forms when \( \Delta\Phi_{ij} < \varepsilon_c \). Stable multi-window coupling produces Coherence Clusters (molecules, organisms, ecosystems, societies).

Core Coherence Domain Classes

Semi-Permeable Coherence Domains (SPCDs)

  • Selective exchange when \( \Delta\Phi < \varepsilon_c \); adaptive boundaries.
  • Enable learning, communication, and evolution. Examples: living cells, cognitive agents, interacting quantum systems, ecological networks.
  • Flux model: \[ I_{ij} = T_{ij}\!\!\int_{\partial \mathcal{W}_i \cap \partial \mathcal{W}_j}\!\!\Psi_i^*\Psi_j\, dA. \]

Rigidly Static Coherence Domains (RSCDs)

  • Zero permeability (\( T_{ij}=0 \)); invariant internal phase (\( d\Psi_i/dt=0 \)).
  • Provide anchoring stability; examples: ideal crystalline matter, frozen field states.
  • Act as reflective barriers to Semi-Permeable Coherence Domains (SPCDs); overabundance induces stagnation.

Expanded Taxonomy of Coherence Domains

Domain Type Symbol Boundary Behaviour Internal Dynamics Ontological Role / Example
Rigidly Static Coherence DomainRSCDCompletely impermeableFixed; no evolutionAbsolute stability; crystals, frozen vacua
Semi-Permeable Coherence DomainSPCDSelective; adaptiveDynamic; self-regulatedCommunication, learning; cells, minds
Dynamically Permeable Coherence DomainDPCDPermeability oscillatesPeriodic updatesRhythmic systems; ecosystems, physiology
Meta-Permeable Coherence DomainMPCDNested layersHierarchical couplingOrganisms, societies, biospheres
Transient Coherence DomainTCDTemporary boundaryRapid form/dissolveReaction intermediates, flashes of thought
Proto-Coherence (Diffuse) DomainPCDIll-defined boundaryLow coherence densityPlasmas, turbulence, pre-biological fields
Hyper-Rigid Coherence DomainHRCDTopologically closedSelf-referential; timelessIdealized black-hole interiors, invariants
Hyper-Permeable Coherence DomainHPCDNearly total permeabilityContinuous phase flowEntanglement webs, collective fields
Equilibrial Coherence DomainECDBalanced permeabilityHomeostatic feedbackStable ecosystems, galactic structures
Transitional Interface DomainTIDHybrid gradientBoundary-layer dynamicsMembranes, phase interfaces

Transmission of Unbound Fractality

Unbound Fractality is inherited across levels: pure in the Metacontinuum; partially constrained in the Differentiat; and regulated dynamically by the Equilibrion (EQB) in complex systems. This inheritance explains persistent multi-scale organization while preserving bounded identity.

Equilibrion Activation Scope

Dimensional scope. In the Pattern Field Theory (PFT) emergence order, the Equilibrion (EQB) does not operate in the pre-spatial stages (first and second dimensions). It becomes active only after the Allen Orbital Lattice (AOL) is established as a spatial coherence scaffold. The Equilibrion regulates multi-domain coherence post-lattice, not during the Metacontinuum or Differentiat stages.

Massless Particle Substrate and Logical Interstices

Dual layer. Instantiated reality exhibits a persistent duality: (i) a massless particle substrate that carries coherence (for example, Pi Particle (π-particle) states and their phase relations), and (ii) the logical interstices—the non-instantiated gaps that retain logical relational potential derived from Unbound Fractality. The substrate supports propagation and stabilization; the interstices preserve capacity for new differentiation.

This duality explains how the universe remains simultaneously coherent (stable patterns) and innovative (capacity for new patterns): Semi-Permeable Coherence Domain (SPCD) exchanges occur on the substrate, while the logical interstices maintain latent possibility.

Fractal Inheritance Principle

Statement. Every physically instantiated particle contains a Fractal Kernel—a bounded, self-similar coherence substructure descending from the first stable fractal (the Pi Particle (π-particle)). Interactions conserve, transmit, or transform kernels but do not eliminate fractality.

Formalization. Let \( \mathcal{R} \) denote the AOL coarse-graining operator and \( \psi_\pi \) the π-particle state. (i) Fixed point: \( \mathcal{R}(\psi_\pi)=\psi_\pi \) with no simpler non-zero fixed point. (ii) Kernel decomposition: any particle field \( \Psi \) admits \( \Psi = \sum_{a} c_{a}\,\mathcal{T}_{a}[\psi_\pi] \), where \( \mathcal{T}_{a} \) are AOL-allowed transforms (translations, rotations, dilations) and \( c_a \) are coherence weights regulated by the Equilibrion (EQB). (iii) Kernel conservation: admissible interactions map kernels to kernels.

Fractality as the Universal Organizer

Axiom (Fractal Organizing Principle). Fractality is the structural mechanism that organizes all coherence within the Pattern Field. It governs how relational potential from the Metacontinuum condenses into the first stable coherence—the Pi Particle (π-particle)—and continues as the recursive organizer of every subsequent domain.

Ontological Role. In the Metacontinuum, unbound fractality represents logical potential. In the Differentiat, it becomes partially bounded, forming distinguishable relations. Within the Pi Particle (π-particle), fractality achieves stable self-similarity, defining the first container of organized mathematical potential. Across the Allen Orbital Lattice (AOL), it governs pattern replication and scaling symmetry, and within the Equilibrion (EQB), it regulates coherence balance across scales to maintain structural stability.

Mathematical Form. Let \( \mathcal{R} \) denote the renormalization or scaling operator on field states. Fractality acts as the invariant organizing constraint: \[ \mathcal{R}^{n}(\Psi) = \lambda^{n} \Psi, \quad \lambda \in \mathbb{R},\ |\lambda|<\infty, \] where the self-similarity factor \( \lambda \) defines the system’s coherence stability range. When \( \mathcal{R}(\Psi) = \Psi \), the pattern is a fixed-point fractal, as in the Pi Particle (π-particle). Higher-order structures are recursive compositions of such invariants.

Summary. Fractality serves as the universal organizer of coherence, determining which configurations can exist and remain stable across scales.

Allen Orbital Lattice — Radial to Vertical Resets via Fractal Windows
Allen Orbital Lattice — Radial → Vertical Resets via Fractal Windows. Radial coherence propagation transitions into vertical layering through Fractal Window Zones (FWZs), producing stable domains within the lattice.

Acronym Quick Index

  • PFT — Pattern Field Theory
  • π-particle — Pi Particle (massless structural invariant)
  • AOL — Allen Orbital Lattice
  • EQB — Equilibrion (dynamic balancer)
  • FWZ — Fractal Window Zone
  • SPCD — Semi-Permeable Coherence Domain
  • RSCD — Rigidly Static Coherence Domain
  • DPCD — Dynamically Permeable Coherence Domain
  • MPCD — Meta-Permeable Coherence Domain
  • TCD — Transient Coherence Domain
  • PCD — Proto-Coherence (Diffuse) Domain
  • HRCD — Hyper-Rigid Coherence Domain
  • HPCD — Hyper-Permeable Coherence Domain
  • ECD — Equilibrial Coherence Domain
  • TID — Transitional Interface Domain

Mathematical Notes

  • Window coupling condition. A channel forms when \( \Delta\Phi_{ij} < \varepsilon_c \).
  • Flux conservation (heuristic). The Equilibrion (EQB) preserves total coherence measure: \[ \sum_i \rho_c(i) \, V_i = \text{const}, \] where \( \rho_c(i) \) is coherence density and \( V_i \) the window measure.
  • Taxonomy parameter space. Domain position is given by \( (\rho_c,\, T,\, \dot{T}) \): density, permeability, and rate of permeability change.

Personal Fractal Window Zones (FWZs)

Human “personal space” is a practical projection of Fractal Window Zone (FWZ) regulation. Safe, low-entropy environments expand \( R_i \); high-entropy or threatening inputs compress it. Social trust and cognitive rapport increase boundary permeability \( T_{ij} \) within the coherence tolerance \( \varepsilon_c \).

Summary: The Continuum of Coherence

All observable structures occupy positions on a spectrum from Rigidly Static Coherence Domains (RSCDs) to Semi-Permeable Coherence Domains (SPCDs) and beyond (dynamic, meta, equilibrial, hyper-states). Pattern interaction is regulated coherence exchange across semi-permeable boundaries. Time indexes coherence updates within Fractal Windows; “universal time” is statistical synchronization. The Equilibrion (EQB) balances these processes across the Allen Orbital Lattice (AOL), conserving global coherence while enabling local evolution.

How to Cite This Article

APA

Allen, J. J. S. (2025). The Taxonomy of Coherence Domains in Pattern Field Theory. Pattern Field Theory. https://www.patternfieldtheory.com/articles/coherence/taxonomy-of-coherence-domains.php

MLA

Allen, James Johan Sebastian. "The Taxonomy of Coherence Domains in Pattern Field Theory." Pattern Field Theory, 2025, https://www.patternfieldtheory.com/articles/coherence/taxonomy-of-coherence-domains.php.

Chicago

Allen, James Johan Sebastian. "The Taxonomy of Coherence Domains in Pattern Field Theory." Pattern Field Theory. October 16, 2025. https://www.patternfieldtheory.com/articles/coherence/taxonomy-of-coherence-domains.php.

BibTeX

@article{allen2025pft,
  author  = {James Johan Sebastian Allen},
  title   = {The Taxonomy of Coherence Domains in Pattern Field Theory},
  journal = {Pattern Field Theory},
  year    = {2025},
  url     = {https://www.patternfieldtheory.com/articles/coherence/taxonomy-of-coherence-domains.php}
}