Key figures (click to enlarge)

AOL trace duplex R=15: prime-log resonance (clean annotated) — Λ-anchored (Duplex), hexR=15 — prime-log resonance; symmetry about *t=0*; gray dots mark *k·log p*.

ECDF vs GUE — Λ-anchored duplex, hexR=15 — ECDF vs GUE — Λ-anchored (Duplex) • hexR=15 • **KS=0.084** • **CvM=0.888**

ECDF vs GUE — π-only surrogate, hexR=15 — ECDF vs GUE — π-only surrogate (control) • hexR=15 • KS=0.455 • CvM=23.907

ECDF vs GUE — PICE variant, hexR=9 — ECDF vs GUE — PICE variant • hexR=9 • **KS=0.138** • **CvM=0.617**

Numerical results (summary)

Run	Anchoring	hexR	Bulk	KS	CvM	Interpretation
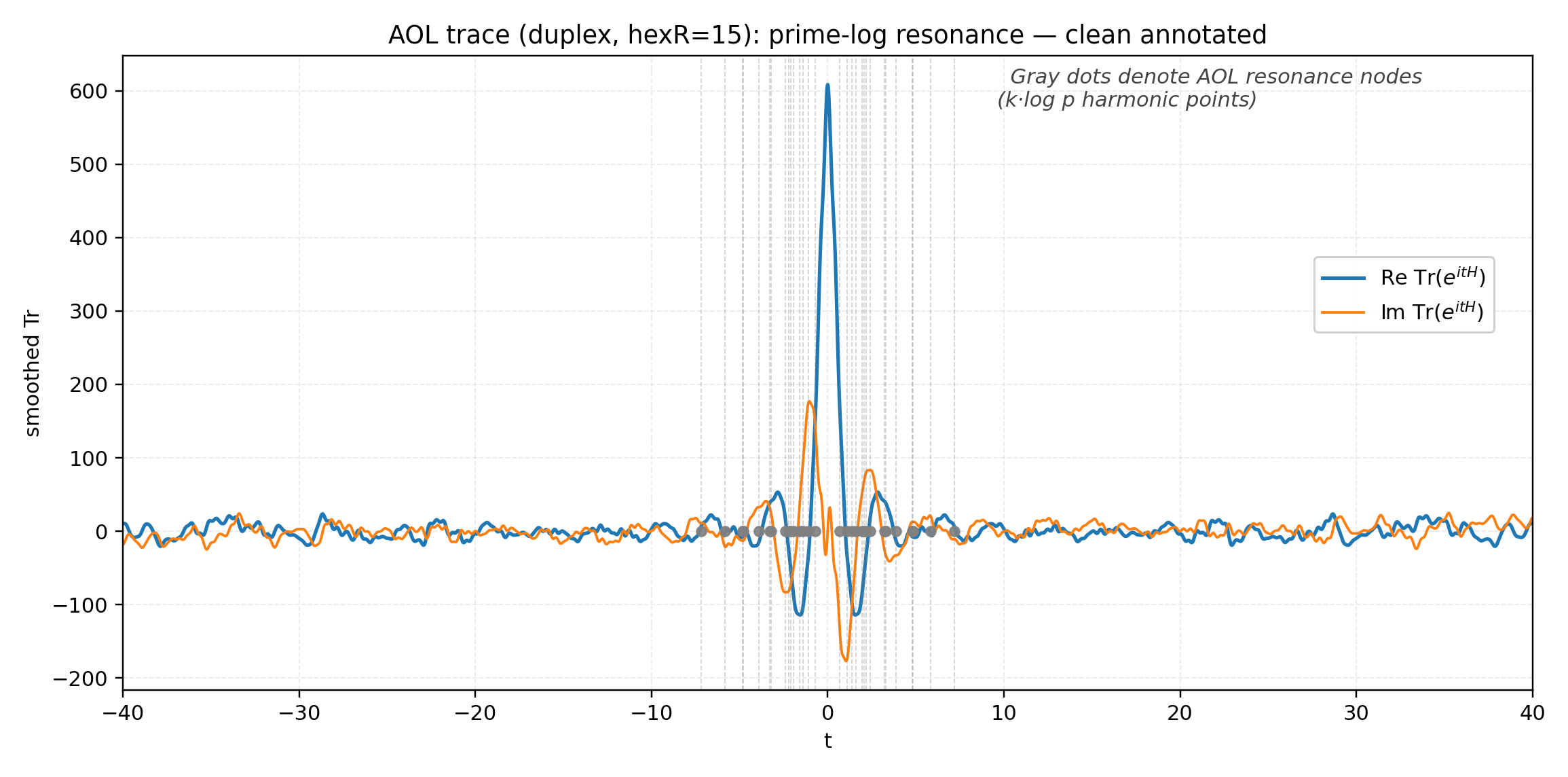
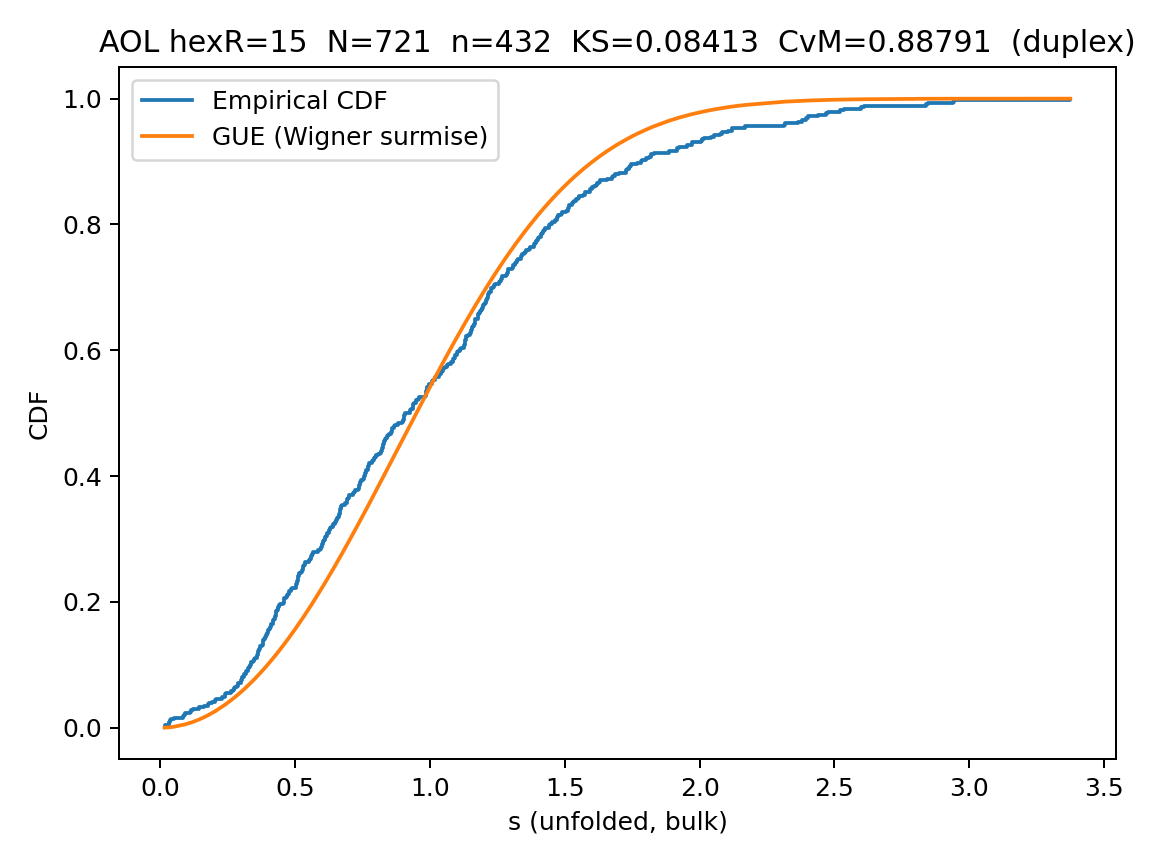
R15 — Duplex (Λ)	Λ(v)=V₀·Λ(f(v))	15	0.20–0.80	0.084	0.888	GUE match; prime-lock coherence
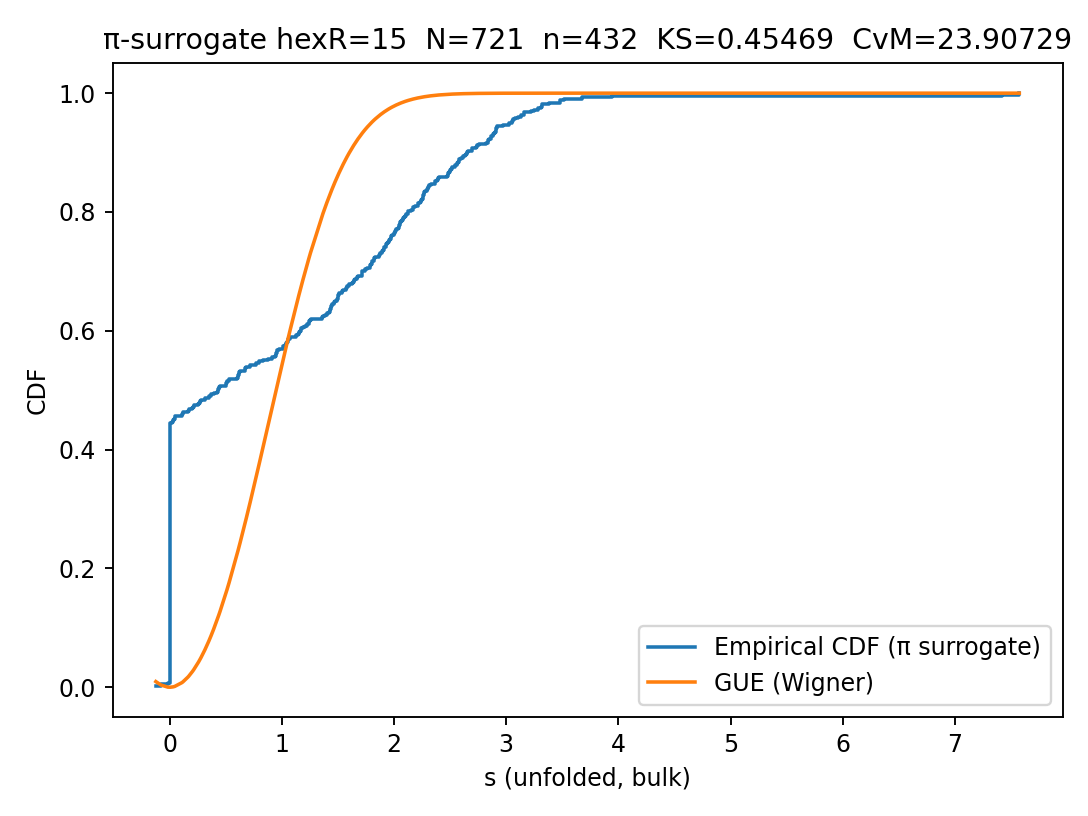
R15 — π surrogate	V(v)=π	15	0.20–0.80	0.455	23.907	No GUE; coherence lost (falsification control)
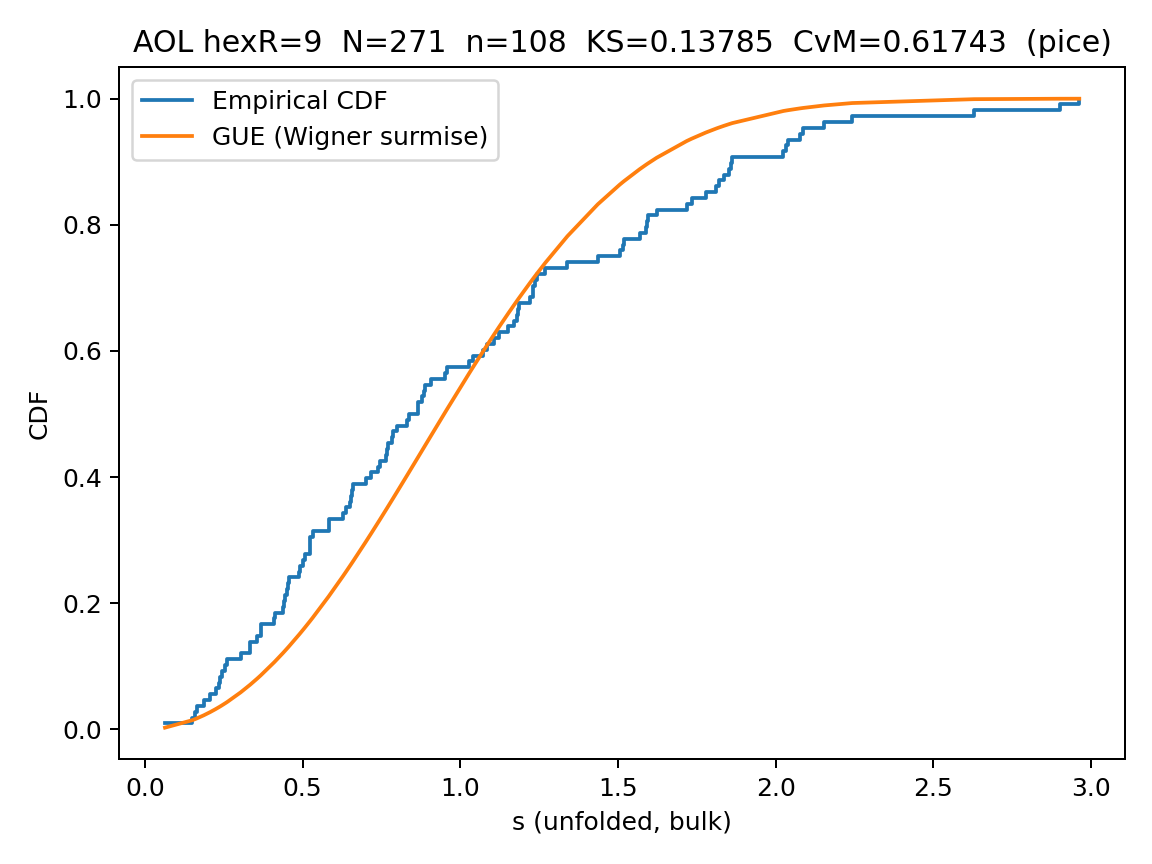
R9 — PICE	curvature-phase (PICE)	9	0.30–0.70	0.138	0.617	Converging equilibrium structure

Method (concise)

AOL acts on the hex-lattice disk of radius R with spiral index map f. Diagonal terms use von Mangoldt anchors, off-diagonals are nearest-neighbor hops with duplex phases \(\theta_{v,w}=2\pi\alpha(\Phi(f(v))+\Phi(f(w)))\) where \(\Phi=\Lambda\) and \(\alpha=1/\varphi\). Bulk eigenvalue spacings are unfolded (quantiles shown), normalized to mean 1, and tested against GUE (Wigner surmise). The trace \(\mathrm{Tr}(e^{itH})\) is evaluated on \([-40,40]\) and lightly smoothed; vertical guides and gray dots mark \(k\log p\) harmonics.

Raw datasets (JSON & CSV)

Λ-anchored (Duplex), hexR=15, bulk 0.20–0.80
- run_R15_duplex_bulk020-080.json
- spacings_R15_duplex_bulk020-080.csv
π-only surrogate (control), hexR=15, bulk 0.20–0.80
- run_R15_pi_bulk020-080.json
- spacings_R15_pi_bulk020-080.csv
PICE variant, hexR=9, bulk 0.30–0.70
- run_R9_pice_bulk030070.json
- spacings_R9_pice_bulk030070.csv

For the complete reproduction pack (code + commands), see the Final Test page.