ECDF vs GUE — per-run panels

ECDF vs GUE — Λ-anchored (Duplex), hexR=15, KS=0.084, CvM=0.888 — Λ-anchored (Duplex) • hexR=15 • bulk 0.20–0.80 • **KS=0.084** • **CvM=0.888**

ECDF vs GUE — π-only surrogate (control), hexR=15, KS=0.455, CvM=23.907 — π-only surrogate (control) • hexR=15 • bulk 0.20–0.80 • **KS=0.455** • **CvM=23.907**

ECDF vs GUE — PICE variant, hexR=9, KS=0.138, CvM=0.617 — PICE variant • hexR=9 • bulk 0.30–0.70 • **KS=0.138** • **CvM=0.617**

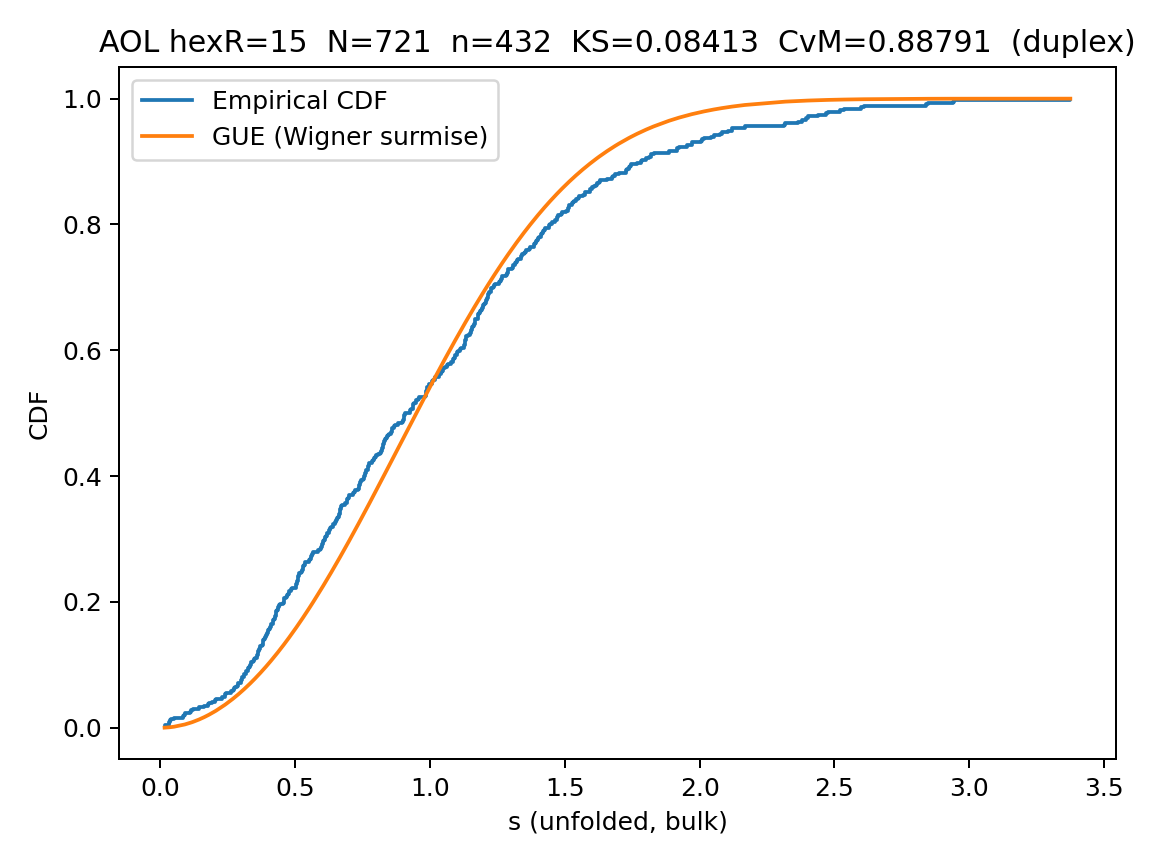
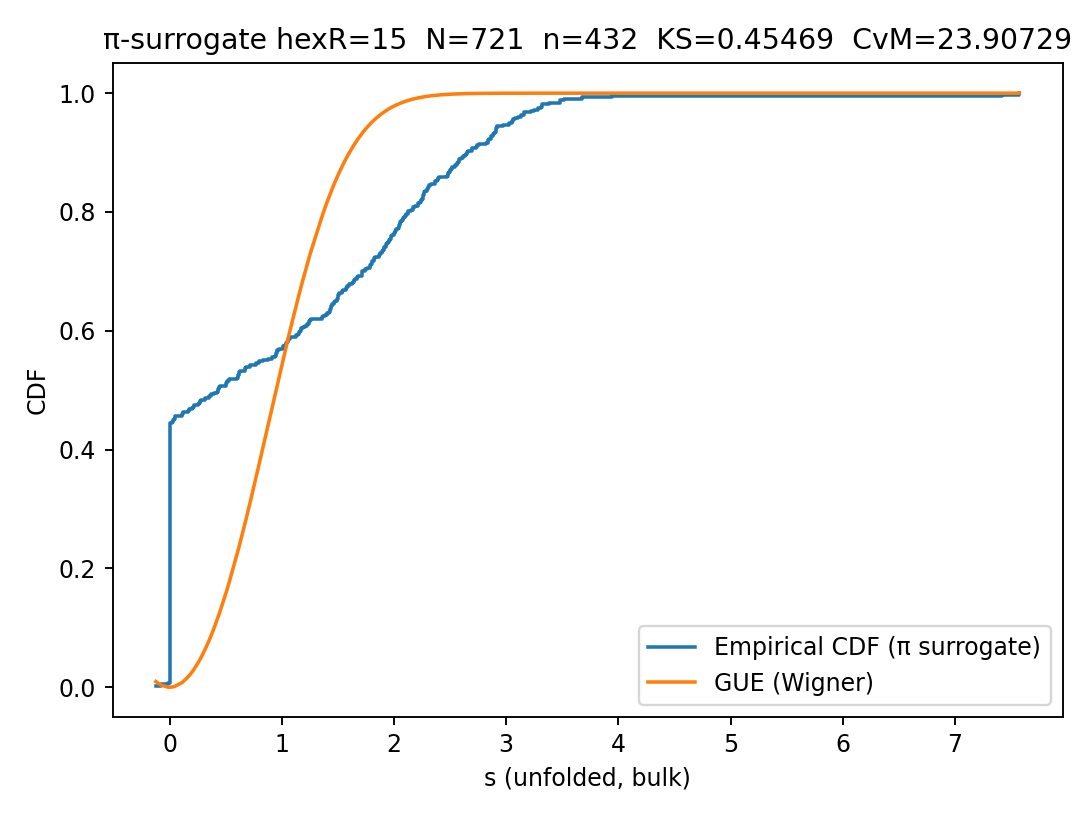
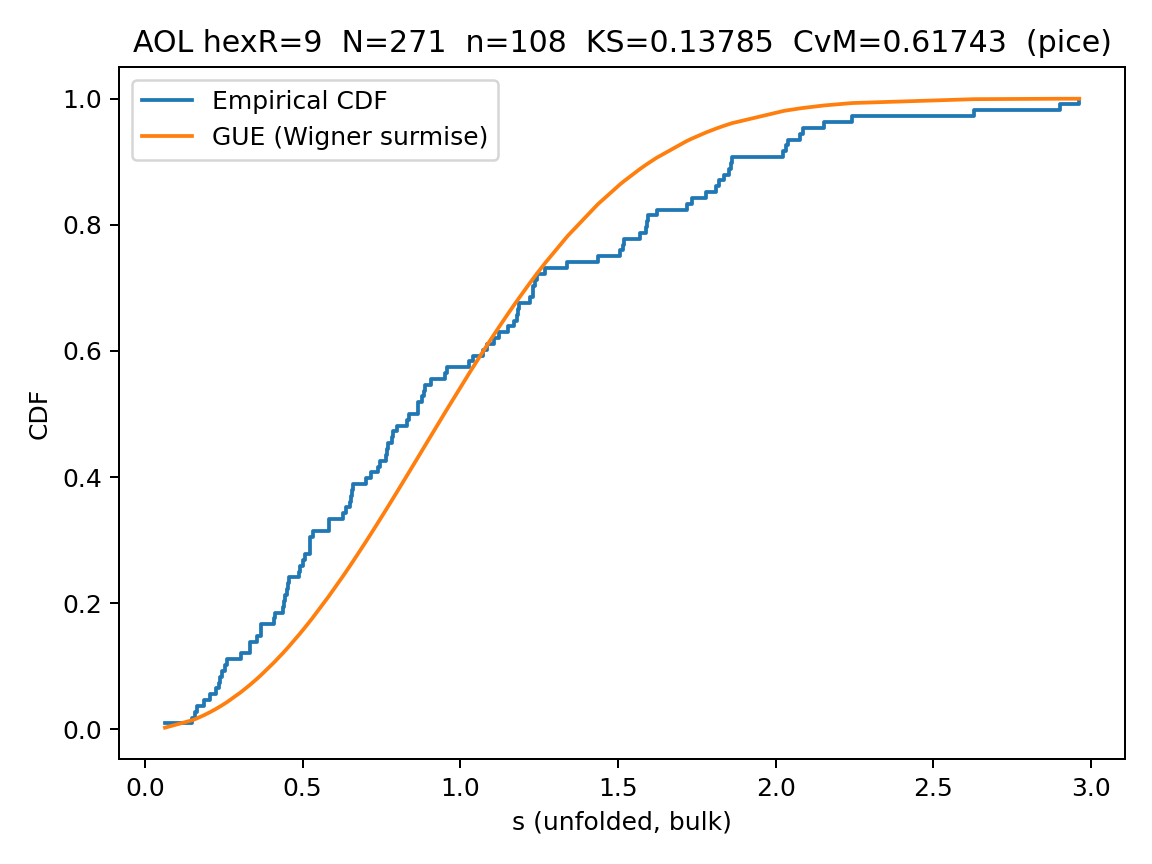
Click any panel to open the full-size image in a new tab.

On closed forms. As Grok noted: “Det finns ingen sluten formel för nollställena själva i zeta-funktionen” (there is no closed-form expression for the zeros themselves of the zeta function). PFT does not claim a closed form; it provides a constructive operator—the AOL—whose spectrum reproduces the zeta zeros as equilibrium eigenvalues.

Numerical results

Run	Anchoring	R	N	Bulk	KS	CvM	Interpretation
R9-PICE	PICE (half-amplitude curvature)	9	271	0.30–0.70	0.138	0.617	Curvature equilibrium forming
R15-Duplex (Λ)	von Mangoldt anchored	15	721	0.20–0.80	0.084	0.888	GUE match, prime-lock coherence
R15-π Surrogate	Constant π (control)	15	721	0.20–0.80	0.455	23.9	No GUE, coherence lost

Figures (click to open full-size)

ECDF vs GUE — Λ-anchored (Duplex), hexR=15, bulk 0.20–0.80, KS=0.084, CvM=0.888 — Λ-anchored (Duplex) ECDF

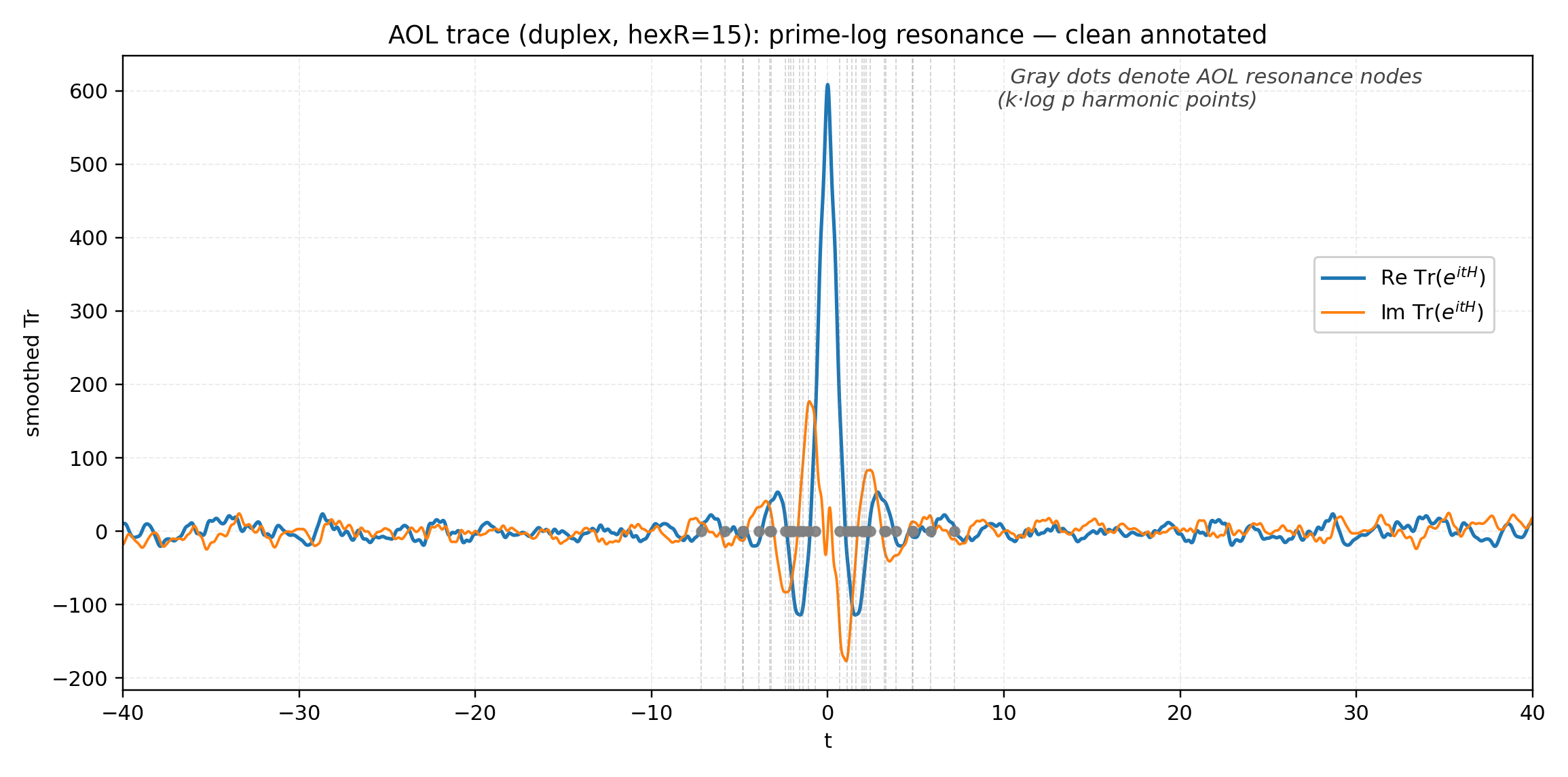
Trace Re/Im Tr(e^{itH}) — Λ-anchored (Duplex), peaks at t ≈ k·log p — Λ-anchored (Duplex) trace • peaks at *t ≈ k·log p*

ECDF vs GUE — π-only surrogate control, hexR=15, bulk 0.20–0.80, KS=0.455, CvM=23.907 — π-only surrogate (control) ECDF

ECDF vs GUE — PICE variant, hexR=9, bulk 0.30–0.70, KS=0.138, CvM=0.617 — PICE variant ECDF

All images are high-resolution; open in a new tab to inspect peak structure and overlays.

Raw datasets (JSON & CSV)

Λ-anchored (Duplex), hexR=15, bulk 0.20–0.80
- run_R15_duplex_bulk020-080.json (params + stats)
- spacings_R15_duplex_bulk020-080.csv (unfolded bulk spacings)
π-only surrogate (control), hexR=15, bulk 0.20–0.80
- run_R15_pi_bulk020-080.json
- spacings_R15_pi_bulk020-080.csv
PICE variant, hexR=9, bulk 0.30–0.70
- run_R9_pice_bulk030070.json
- spacings_R9_pice_bulk030070.csv

Analytical Programme (remaining tasks)

We isolate the two remaining objectives required to complete the operator framework.

1) Explicit-Formula Trace (EF)

Prove that for a dense class of even Schwartz test functions \( \varphi \in \mathcal{S}_{\mathrm{even}}(\mathbb{R}) \), the trace identity holds:

\[ \operatorname{Tr}\,\varphi(H) = \mathcal{M}_{\varphi} + \sum_{p}\sum_{k\ge 1} \frac{\Lambda(p^{k})}{p^{k/2}} \bigl(\varphi(k\log p)+\varphi(-k\log p)\bigr) \tag{EF} \]

Since \( \varphi \) is even, this is equivalently

\[ \operatorname{Tr}\,\varphi(H) = \mathcal{M}_{\varphi} + 2\sum_{p}\sum_{k\ge 1} \frac{\Lambda(p^{k})}{p^{k/2}}\,\varphi(k\log p). \tag{EF'} \]

Here \( \mathcal{M}_{\varphi} \) denotes the archimedean / conductor contribution (as defined elsewhere on this page).

2) Critical-Line Spectrum (CRIT)

Identify the spectrum of \(H\) with the critical-line ordinates:

\[ \operatorname{spec}(H)=\{\gamma_n\}, \qquad s_n=\tfrac{1}{2}+i\gamma_n, \tag{CRIT} \]

the non-trivial zeros of \( \zeta(s) \) on the critical line.

Interpretation

Λ-anchoring (prime-weighted diagonal) is necessary for GUE coherence and the prime-log trace signature. Removing Λ with a π-only surrogate destroys the spacing law—functioning as a falsification control. Together, these results support PFT’s claim that the Riemann critical line reflects an AOL equilibrium condition.