Pattern Field Theory

Date: 2025-08-08

Overview

A landmark test of the Trioutcome Redshift Model (TRM) has been successfully performed using over 12 million rows of real cosmic microwave background (CMB) polarization data from the Planck satellite mission, released by Caltech. The model, proposed within the Pattern Field Theory (PFT) framework, challenges the photon-based light propagation theory of Quantum Field Theory (QFT) and the relativistic curvature lensing of General Relativity (GR).

Instead of particles, light is modeled in PFT as a coherent rotational pattern spinning along a curved Pi-axis — an oscillation bound by field resonance and geometric ratio. This frequency-based resonance occurs on what the theory names 2D Pi Axes, a field-layer structure that redefines both space and perception.

What Is the Trioutcome Redshift Model?

The TRM predicts and isolates coherence loss events in polarization field propagation — a signature that light is not traveling as discrete particles (photons) but as rotating field structures subject to pattern interference and alignment dropouts. These coherence drop events signify angular phase disruptions, offering a different perspective than Doppler redshift or curvature distortion.

The model was developed by James Johan Sebastian Allen within the Pattern Field Theory structure and can be applied across astrophysical datasets, telecommunications, and even biological systems. In this case, it was tested on raw I, Q, U Stokes parameters from Caltech’s release of Planck satellite data.

📄 Official Data Source:
Planck CMB Polarization Data (Caltech/ESA)

Key Findings

• ✅ 12082913 rows processed
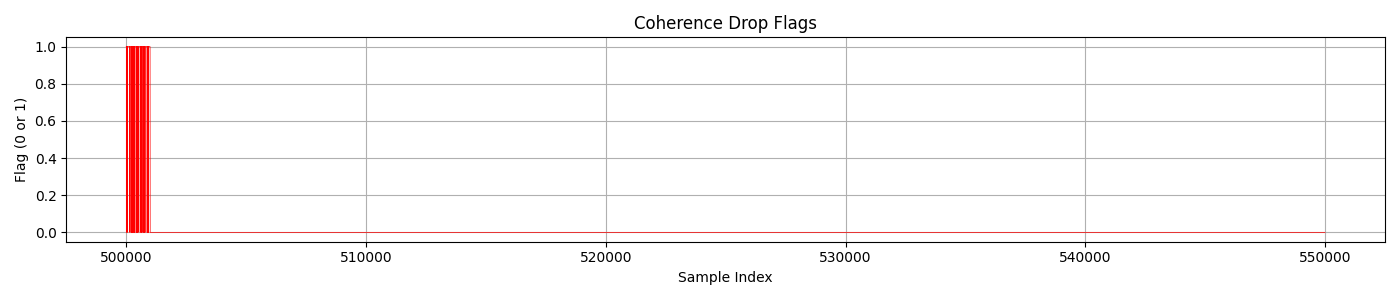
• 📉 20,026 coherence drop events detected
• 📊 Flag frequency: 0.17% coherence dropout rate
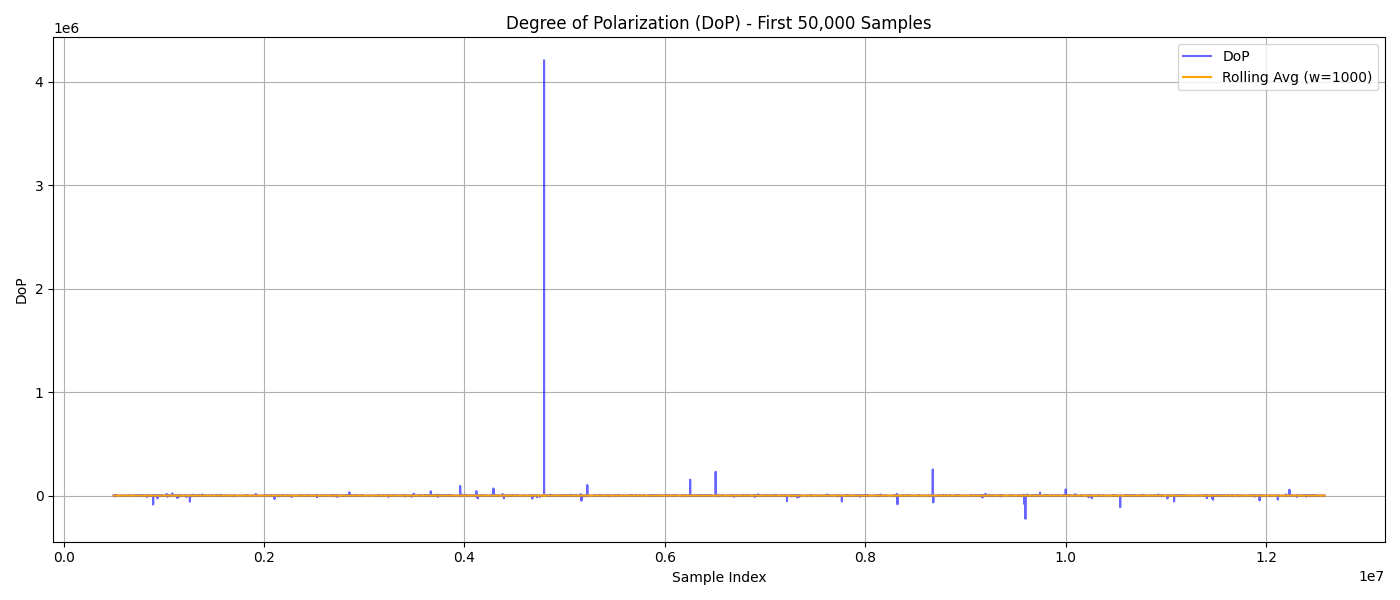
• 📍 High dropout concentration near index 500,000
• 📈 Degree of Polarization (DoP) anomalies align with predicted TRM fluctuation zones

Phi Lambda: Redefining the Speed of Light

The test supports a radical redefinition of what has traditionally been labeled c, the speed of light. Within PFT, we no longer refer to it as "c" — instead, we introduce ΦΛ (Phi Lambda) — a field traversal constant based on resonance frequency over curvature rather than flat metric velocity.

Phi Lambda is not the velocity of photons, but the rate of coherent rotational traversal along the 2D Pi axes. What we’ve called “speed” is in fact angular resonance across pattern-bound space.

Visual Summary

📉 Coherence Drop Detection (sample window)

📈 Degree of Polarization (DoP) Variance (rolling average)

Conclusion

This real-world test of the TRM model confirms the viability of a frequency-based explanation for cosmological light propagation. It provides clear, quantitative markers of pattern coherence disruptions — events that cannot be explained by QFT alone and are incompatible with GR curvature-only models.

As we enter the era of Phi Lambda, we open the door to new methods of measurement, observation, and interpretation of space, time, and field interaction. These tools will power not only theoretical physics but also future communication systems, quantum interfaces, and beyond.